题目内容
13.在公差大于0的等差数列{an}中,2a7-a13=1,且a1,a3-1,a6+5成等比数列,则数列{(-1)n-1an}的前21项和为( )| A. | 21 | B. | -21 | C. | 441 | D. | -441 |
分析 设公差为d(d>0),运用等差数列的通项公式,可得首项为1,再由等比数列的中项的性质,解方程可得公差d,进而得到等差数列{an}的通项,再由并项求和即可得到所求和.
解答 解:公差d大于0的等差数列{an}中,2a7-a13=1,
可得2a1+12d-(a1+12d)=1,即a1=1,
a1,a3-1,a6+5成等比数列,
可得(a3-1)2=a1(a6+5),
即为(1+2d-1)2=1+5d+5,
解得d=2(负值舍去)
则an=1+2(n-1)=2n-1,n∈N*,
数列{(-1)n-1an}的前21项和为a1-a2+a3-a4+…+a19-a20+a21=1-3+5-7+…+37-39+41
=-2×10+41=21.
故选:A.
点评 本题考查数列的求和,注意运用并项求和,考查等差数列的通项公式和等比数列的中项的性质,考查运算能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的左焦点为F,直线x=a与椭圆相交于点M、N,当△FMN的周长最大时,△FMN的面积是( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
1.已知随圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4$\sqrt{3}$,则椭圆E的焦距的取值范围是( )
| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |
8.已知实数x,y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y-4≥0\\ 2x-y-5≤0\end{array}\right.$,若使得目标函数z=ax+y取最大值的最优解有无数个,则实数a的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
5. 已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
 已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )| A. | x2=4y | B. | x2=2$\sqrt{3}$y | C. | x2=6y | D. | x2=2$\sqrt{2}$y |
3.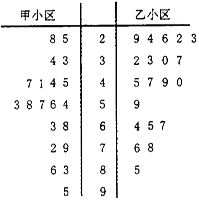 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
(1)求甲小区和乙小区的中位数;
(2)身体综合素质测试成绩在60分以上(含60)的人称为“身体综合素质良好”,否则称为“身体综合素质一般”.以样本中的频率作为概率,两小区人口都按1000人计算,填写下列2×2列联表,
并判断是否有97.5%把握认为“身体综合素质良好”与“小区是否建设健身广场”有关?
(附:k=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:(1)求甲小区和乙小区的中位数;
(2)身体综合素质测试成绩在60分以上(含60)的人称为“身体综合素质良好”,否则称为“身体综合素质一般”.以样本中的频率作为概率,两小区人口都按1000人计算,填写下列2×2列联表,
| 甲小区(有健康广场) | 乙小区(无健康广场) | 合计 | |
| 身体综合素质良好 | 350 | 300 | 650 |
| 身体综合素质一般 | 650 | 700 | 1350 |
| 合计 | 1000 | 1000 | 2000 |
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 1.706 | 3.841 | 5.024 | 6.635 | 7.879 |
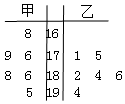 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: