题目内容
2.已知圆C:x2+y2+2x-8y+m=0与抛物线上E:y2=8x的准线l相切,抛物线E上的点P到准线l的距离为d,Q为圆C上任意一点,则|PQ|+d的最小值等于( )| A. | 3 | B. | 2 | C. | 4 | D. | 5 |
分析 圆C:x2+y2+2x-8y+m=0与抛物线上E:y2=8x的准线l相切,求出圆心与半径,抛物线y2=8x的准线为l:x=-2,焦点为F(2,0),当P,Q,F三点共线时,P到点Q的距离d与点P到抛物线的焦点距离|PQ|之和最小,从而d+|PQ|的最小值为|FC|-r.
解答 解:圆C:x2+y2+2x-8y+m=0配方,得(x+1)2+(y-4)2=17-m,圆心为C(-1,4),半径r=$\sqrt{17-m}$.
∵圆C与抛物线上E:y2=8x的准线l相切,∴$\sqrt{17-m}$=1,∴m=16
如图所示,由题意,知抛物线y2=8x的焦点为F(2,0),连接PF,则d=|PF|.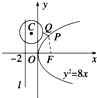
d+|PQ|=|PF|+|PQ|,显然,|PF|+|PQ|≥|FQ|(当且仅当F,P,Q三点共线时取等号).
而|FQ|为圆C上的动点Q到定点F的距离,
显然当F,Q,C三点共线时取得最小值,
最小值为|CF|-r=$\sqrt{(-1-2)^{2}+(4-0)^{2}}$-1=5-1=4.
故选:C.
点评 本题考查线段和的最小值的求法,考查抛物线的定义,是中档题,正确转化是关键.

练习册系列答案
相关题目
12.已知△ABC中,D为BC边上一点,∠BAD=∠CAD,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=2,∠BAC=$\frac{π}{3}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=( )
| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |
13.在公差大于0的等差数列{an}中,2a7-a13=1,且a1,a3-1,a6+5成等比数列,则数列{(-1)n-1an}的前21项和为( )
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |
7.已知复数z满足$\frac{1+i}{1-i}$•z=3+4i,则z的共轭复数为( )
| A. | 4+3i | B. | -4+3i | C. | -4-3i | D. | 4-3i |