题目内容
已知f(x)的定义域为R,满足f(x)=-f(-x),且x>0时,f(x)=2x-x2.
(1)求f(x)的解析式;
(2)是否存在正数m、n,当x∈[m,n]时,g(x)=f(x),且g(x)的值域为[
,
].
(1)求f(x)的解析式;
(2)是否存在正数m、n,当x∈[m,n]时,g(x)=f(x),且g(x)的值域为[
| 1 |
| n |
| 1 |
| m |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)设x<0,则-x>0,运用求解f(x)=-f(-x),且x>0时,f(x)=2x-x2.(2)根据二次函数的性质,分类求解
.
.
解答:
解:(1)∵f(x)的定义域为R,满足f(x)=-f(-x),∴f(0)=0
∵x>0时,f(x)=2x-x2.
∴设x<0,则-x>0,
∴f(x)=-f(-x)=-[-2x-x2]=x2+2x,(x<0)
∴f(x)=
,
(2)g(x)=2x-x2,x>0
(Ⅱ)g(x)=f(x)=2x-x2=-(x-1)2+1≤1,
又m>0,n>0,
∴
≤1,m≥1,即1≤m<n,f(x)为减函数,
于是
=g(n)=-n2+2n,即(n-1)(n2-n-1)=0,
∴
=g(m)=-m2+2m,即(m-1)(m2-m-1)=0,
∵1≤m<n,
∴m=1,n=
∵x>0时,f(x)=2x-x2.
∴设x<0,则-x>0,
∴f(x)=-f(-x)=-[-2x-x2]=x2+2x,(x<0)
∴f(x)=
|
(2)g(x)=2x-x2,x>0
(Ⅱ)g(x)=f(x)=2x-x2=-(x-1)2+1≤1,
又m>0,n>0,
∴
| 1 |
| m |
于是
| 1 |
| n |
∴
| 1 |
| m |
∵1≤m<n,
∴m=1,n=
1+
| ||
| 2 |
点评:本题考查了二次函数的性质,分类讨论的思想,属于中档题.

练习册系列答案
相关题目
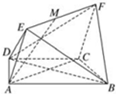 如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=
如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=