题目内容
在△ABC中，a=4，b=6
，A=30°，则此三角形解的情况是 （ ）
| 2 |
| A、一解 | B、两解 |
| C、一解或两解 | D、无解 |
考点：正弦定理
专题：计算题,解三角形
分析：由正弦定理可得
=
，解得sinB的值，即可得出结论．
| 4 | ||
|
6
| ||
| sinB |
解答：
解：∵△ABC中，a=4，b=6
，A=30°，
则由正弦定理可得
=
解得sinB=
＞1．
故此三角形解的情况是：无解，
故选：D．
| 2 |
则由正弦定理可得
| 4 | ||
|
6
| ||
| sinB |
解得sinB=
3
| ||
| 4 |
故此三角形解的情况是：无解，
故选：D．
点评：本题给出三角形的两条边和一个角，判断三角形的解有几个．着重考查了正弦定理和已知三角函数求角等知识，属于中档题．
练习册系列答案
相关题目
若x02＞2py0（p＞0），则称点（x0，y0）在抛物线C：x2=2py（p＞0）外．已知点P（a，b）在抛物线C：x2=2py（p＞0）外，则直线l：ax=p（y+b）与抛物线C的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、不能确定 |
一个空间几何体的三视图如图所示，该几何体的表面积为（ ）
| A、96 | B、136 |
| C、152 | D、192 |
已知α：|z|≤1，z∈C，β：|z-i|≤a，z∈C．若α是β的充分非必要条件，则实数a的取值范围是（ ）
| A、a≥1 | B、a≤1 |
| C、a≥2 | D、a≤2 |
已知a＞0且a≠1，则在下面所给出的四种图形中，正确表示函数y=ax和y=logax的图象一定是（ ）
| A、①③ | B、②③ | C、②④ | D、①④ |
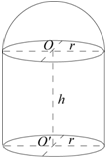要设计一个金属容积为V（常数）的密闭容器，下部是圆柱形，上部为半球形（如图）．当圆柱底面半径r与高h各为何值时，制造这个容器用料最省（表面积最小）？