题目内容
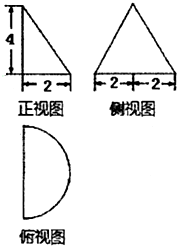
一个空间几何体的三视图如图所示，该几何体的表面积为（ ）
| A、96 | B、136 |
| C、152 | D、192 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体为三棱柱，关键三视图判断三棱柱的侧棱长及底面三角形的形状，求出底面三角形的腰长，把数据代入棱柱的表面积公式计算．
解答：
解：由三视图知；几何体为三棱柱，且三棱柱的侧棱长为8，
底面为等腰三角形，底边长为6，高为4，腰长5，
∴几何体的表面积S=2×
×6×4+（5+5+6）×8=24+128=152．
故选：C．
底面为等腰三角形，底边长为6，高为4，腰长5，
∴几何体的表面积S=2×
| 1 |
| 2 |
故选：C．
点评：本题考查了由三视图求几何体的表面积，判断三视图的数据所对应的几何量是关键．
练习册系列答案
名校课堂系列答案
相关题目
已知i为虚数单位，复数z=
，则z=（ ）
| 1+i |
| 1-i |
| A、i | B、1 | C、-1 | D、-i |
等比数列的前n项，前2n项，前3n项的和分别是A，B，C，则（ ）
| A、（A+B）-C=B2 |
| B、A2+B2=A（B+C） |
| C、A+B=C |
| D、B2=AC |
已知集合A={x|x-2＞0}，B={1，2，3，4}，则（∁RA）∩B=（ ）
| A、{1} |
| B、{1，2} |
| C、{2，3} |
| D、{2，3，4} |
一个几何体的三视图如图所示，则这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
为了得到函数y=sin（3x+
）的图象，只需将函数y=sinx的图象上所有的点（ ）
| π |
| 3 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向左平移
| ||||
D、向左平移
|
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，其中甲成绩的中位数为15，极差为12；乙成绩的众数为13，. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，a=4，b=6
，A=30°，则此三角形解的情况是 （ ）
| 2 |
| A、一解 | B、两解 |
| C、一解或两解 | D、无解 |