题目内容
18.${(\sqrt{2x}+\frac{1}{x^2})^n}$展开式中只有第六项二项式系数最大,则展开式中的常数项是720.分析 由条件利用二项式系数的性质求得n=10,再利用二项式展开式的通项公式,求得展开式中的常数项.
解答 解:由题意可得${C}_{n}^{5}$最大,故n=10,故${(\sqrt{2x}+\frac{1}{x^2})^n}$=${(\sqrt{2x}+\frac{1}{{x}^{2}})}^{10}$,
它的展开式的通项公式为Tr+1=${C}_{10}^{r}$•${(\sqrt{2})}^{10-r}$•${x}^{\frac{10-5r}{2}}$,
令$\frac{10-5r}{2}$=0,求得r=2,故展开式中的常数项是${C}_{10}^{2}$•${(\sqrt{2})}^{8}$=720,
故答案为:720.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
8.已知命题p:?x0∈R,x0-2>0,命题q:?x∈R,2x>x2,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
6.设集合A={x|x2-2x≤0},B={y|y=x2-2x},则A∩B=( )
| A. | [-1,2] | B. | [0,2] | C. | [-1,+∞) | D. | [0,+∞) |
13.函数f(x)=$\frac{1}{2}$sin2x+$\frac{1}{2}$tan$\frac{π}{3}$cos2x的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
10.若△ABC的三条边a、b、c满足(a+b):(b+c):(c+a)=7:9:10,则△ABC( )
| A. | 一定是锐角三角形 | |
| B. | 一定是直角三角形 | |
| C. | 一定是钝角三角形 | |
| D. | 可能是锐角三角形也可能是钝角三角形 |
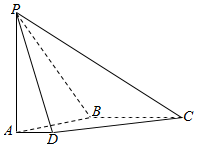 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.