题目内容
2.若M为抛物线y=2x2第一象限上的点,且M到焦点的距离为$\frac{1}{4}$,则M的坐标为$({\frac{1}{4},\frac{1}{8}})$.分析 求得抛物线的焦点坐标,由抛物线的焦点弦公式,即可求得y0,代入抛物线方程,即可求得M点坐标.
解答 解:抛物线标准方程x2=$\frac{1}{2}$y,即2p=$\frac{1}{2}$,则p=$\frac{1}{4}$,$\frac{p}{2}$=$\frac{1}{8}$,则焦点F(0,$\frac{1}{8}$),
由M(x0,y0)到焦点的距离d=y0+$\frac{p}{2}$=$\frac{1}{4}$,即y0=$\frac{1}{8}$,
则x02=$\frac{1}{2}$y0,解得x0=±$\frac{1}{4}$,
由M在第一象限,则x0=$\frac{1}{4}$,
M的坐标为$({\frac{1}{4},\frac{1}{8}})$,
故答案为:$({\frac{1}{4},\frac{1}{8}})$.
点评 本题考查抛物线的简单几何性质,抛物线的焦点弦公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若角θ满足条件sinθcosθ<0,且cosθ-sinθ<0,则θ在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.若(x2-1)+(x+1)i是纯虚数,则实数x的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 以上都不对 |
7. 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
请你根据频率分布表解答下列问题:
(1)求出频率分布表中①、②、③、④、⑤处的值;
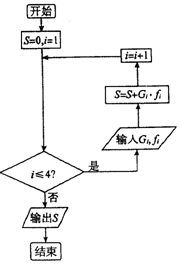
(2)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序功能是什么?求输出S的值.
 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
(1)求出频率分布表中①、②、③、④、⑤处的值;
(2)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序功能是什么?求输出S的值.
11.已知△ABC和平面上一点O满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,若存在实数λ使得$\overrightarrow{AB}$=λ$\overrightarrow{OA}$-$\overrightarrow{AC}$,则λ=( )
| A. | -3 | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | 3 |
12.△ABC中,角A、B、C所对的边分别是a、b、c,若a=2,b=3,$c=\sqrt{5}$,则cosC=( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |