△ABC中.角A.B.C所对的边分别是a.b.c.若a=2.b=3.$c=\sqrt{5}$.则cosC=( )A．$\frac{2}{3}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

12．△ABC中，角A、B、C所对的边分别是a、b、c，若a=2，b=3，$c=\sqrt{5}$，则cosC=（　　）

A．

$\frac{2}{3}$

B．

$\frac{2}{5}$

C．

$\frac{3}{5}$

D．

$\frac{4}{5}$

分析直接利用余弦定理化简求解即可．

解答解：△ABC中，角A、B、C所对的边分别是a、b、c，若a=2，b=3，$c=\sqrt{5}$，
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4+9-5}{2×2×3}$=$\frac{2}{3}$．
故选：A．

点评本题考查余弦定理的应用，考查计算能力．

练习册系列答案

3．设向量$\overrightarrow a$，$\overrightarrow b$不共线，$（λ\overrightarrow a+\overrightarrow{b）}$与（$\overrightarrow a$+$2\overrightarrow b$）共线，则实数λ的值为$\frac{1}{2}$．

20．已知f（x）是定义在R上的偶函数，在[0，+∞）上单调增，且f（2）=1，则满足f（x-1）＞1的x的取值范围是（-∞，-1）∪（3，+∞）．

7．已知函数f（x）=$\frac{{2}^{x}-a•{2}^{x}}{{2}^{x}+{2}^{-x}}$是定义R在上的奇函数．
（1）求实数a的值，并求函数f（x）的值域；
（2）设g（x）=（2^x+2^-x）•f（x）．
（ⅰ）判断函数y=g（x）的单调性（不需要说明理由），并求使不等式g（x²+tx）+g（4-x）＞0对x∈R恒成立的实数t的取值范围；
（ⅱ）设h（x）=2^2x+2^-2x-2m•g（x）且h（x）在[1，+∞）上的最小值为-2，求实数m的值．

17．已知$\overrightarrow a=（2，4），\overrightarrow b=（x，-2），且\overrightarrow a∥\overrightarrow b$，则x=-1．

4．

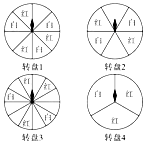如图，是四个可以自由转动的转盘，转盘被平均分成若干个扇形，转动转盘，转盘停止后，有两个转盘的指针指向白色区域的概率相同，则这两个转盘是（　　）

1．若向量$\overrightarrow{a}$、$\overrightarrow{b}$ 满足|$\overrightarrow{a}$|=$\sqrt{2}$，|$\overrightarrow{b}$|=1，$\overrightarrow{a}•\overrightarrow{b}$=-1，则向量$\overrightarrow{a}$、$\overrightarrow{b}$ 的夹角的大小为$\frac{3π}{4}$．

2．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1（0≤x≤1）}\\{f（x-1）+m（x＞1）}\end{array}\right.$在定义域[0，+∞）上单调递增，且对于任意a≥0，方程f（x）=a有且只有一个实数解，则函数g（x）=f（x）-x在区间[0，2ⁿ]（n∈N^*）上所有零点的和为（　　）

$\frac{（1+{2}^{n}）^{2}}{2}$

D．

2ⁿ-1

试题分类