设函数f=2.则f(2)=4．题目和参考答案——青夏教育精英家教网—

题目内容

14．设函数f（x）=ax+b，若f（1）=f'（1）=2，则f（2）=4．

分析由已知得f′（x）=a，从而列出方程组，求出a，b，由此能求出f（x）=2x，进而能求出f（2）．

解答解：∵函数f（x）=ax+b，f（1）=f'（1）=2，
∴f′（x）=a，
∴$\left\{\begin{array}{l}{f（1）=a+b=2}\\{{f}^{'}（1）=a=2}\end{array}\right.$，解得a=2，b=0，
∴f（x）=2x，
∴f（2）=2×2=4．
故答案为：4．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意导数、函数性质的合理运用．

练习册系列答案

口算心算速算天天练江苏人民出版社系列答案

5．下列数据中，拟合效果最好的回归直线方程，其对应的相关指数R²为（　　）

2．若M为抛物线y=2x²第一象限上的点，且M到焦点的距离为$\frac{1}{4}$，则M的坐标为$（{\frac{1}{4}，\frac{1}{8}}）$．

9．已知函数f（x）=sinx，g（x）=e^x•f'（x），其中e为自然对数的底数．
（1）求曲线y=g（x）在点（0，g（0））处的切线方程；
（2）若对任意$x∈[{-\frac{π}{2}，0}]$，不等式g（x）≥x•f（x）+m恒成立，求实数m的取值范围；
（3）试探究当$x∈[{\frac{π}{4}，\frac{π}{2}}]$时，方程g（x）=x•f（x）的解的个数，并说明理由．

19．设函数f（x）=ln（1+x）-$\frac{2x}{x+2}$，证明：当x＞0时，f（x）＞0．

6．若a₁＞0，a₁≠1，a_n+1=$\frac{2{a}_{n}}{1+{a}_{n}}$（n=1，2，…）．
（1）求证：a_n+1≠a_n；
（2）令a₁=$\frac{1}{2}$，写出a₂，a₃，a₄，a₅的值，观察并归纳出这个数列的通项公式a_n，并用数学归纳法证明．

3．设向量$\overrightarrow a$，$\overrightarrow b$不共线，$（λ\overrightarrow a+\overrightarrow{b）}$与（$\overrightarrow a$+$2\overrightarrow b$）共线，则实数λ的值为$\frac{1}{2}$．

4．

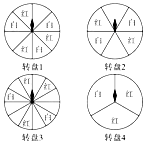如图，是四个可以自由转动的转盘，转盘被平均分成若干个扇形，转动转盘，转盘停止后，有两个转盘的指针指向白色区域的概率相同，则这两个转盘是（　　）

试题分类