题目内容
11.已知△ABC和平面上一点O满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,若存在实数λ使得$\overrightarrow{AB}$=λ$\overrightarrow{OA}$-$\overrightarrow{AC}$,则λ=( )| A. | -3 | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | 3 |
分析 根据题意O是三角形的重心,同时存在实数λ使得$\overrightarrow{AB}$+$\overrightarrow{AC}$=λ$\overrightarrow{OA}$,成立,则可知根据三角形重心的性质,$\overrightarrow{AO}$=$\frac{2}{3}$$\overrightarrow{AD}$,那么解得λ=-3.
解答 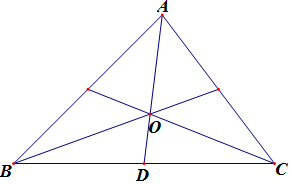 解:根据题意,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则可知点M是三角形的重心,
解:根据题意,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则可知点M是三角形的重心,
同时存在实数λ使得$\overrightarrow{AB}$+$\overrightarrow{AC}$=λ$\overrightarrow{OA}$,成立,则可知$\overrightarrow{AO}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),即$\overrightarrow{AB}$+$\overrightarrow{AC}$=3$\overrightarrow{AO}$,
由$\overrightarrow{AO}$=-$\overrightarrow{OA}$,则m=-3,
故选:A.
点评 本题考查三角形的重心的性质,向量的加法,考查计算能力,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
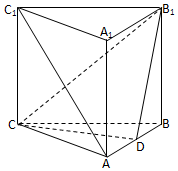 如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点
如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点