题目内容
已知向量
=(1,2),
=(x,1),
=
+2
,
=2
-
.
(1)当
∥
时,求x的值;
(2)当
⊥
时,求x的值.
| a |
| b |
| u |
| a |
| b |
| v |
| a |
| b |
(1)当
| u |
| v |
(2)当
| u |
| v |
考点:平面向量数量积的运算,平面向量的坐标运算
专题:平面向量及应用
分析:(1)通过
∥
,列出方程求出x的值即可;
(2)当
⊥
时,转化为数量积为0,列出方程求x的值.
| u |
| v |
(2)当
| u |
| v |
解答:
解:向量
=(1,2),
=(x,1),
=
+2
=(1+2x,4),
=2
-
=(2-x,3)…(2分)
(1)当
∥
时,则3(1+2x)=4(2-x),得x=
…(6分)
(2)当
⊥
时,则(1+2x)(2-x)+12=0,解得x=-2或
…(10分)
| a |
| b |
| u |
| a |
| b |
| v |
| a |
| b |
(1)当
| u |
| v |
| 1 |
| 2 |
(2)当
| u |
| v |
| 7 |
| 2 |
点评:本题考查向量的平行以及向量的垂直充要条件的应用,数量积的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a>0,设p:存在a∈R,使y=ax是R上的单调递减函数; q:存在a∈R,使函数g(x)=lg(2ax2+2x+1)的值域为R,如果“p∧q”为假,“p∨q”为真,则a的取值范围是( )
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
 如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)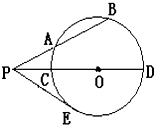 如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7
如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7