题目内容
在△ABC中,BC=2,B=
,当△ABC的面积等于
时,AB=( )
| π |
| 3 |
| ||
| 2 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用三角形面积公式列出关系式,将BC,sinB,以及已知面积代入求出AB的长即可.
解答:
解:∵在△ABC中,BC=2,B=
,△ABC的面积等于
,
∴S△ABC=
AB•BC•sinB=
,即
×AB×2×
=
,
解得:AB=1,
故选:C.
| π |
| 3 |
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解得:AB=1,
故选:C.
点评:此题考查了三角形的面积公式,以及特殊角的三角函数值,熟练掌握三角形面积公式是解本题的关键.

练习册系列答案
相关题目
“直线y=kx+b过点(1,1)”是“k=2且b=-1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=x2-tan(
-α)•x+1在[
,+∞)上单调递增,则α的取值范围是( )
| π |
| 6 |
| ||
| 2 |
A、[kπ-
| ||||
B、(kπ-
| ||||
C、(-
| ||||
D、(-∞,kπ+
|
一位生物学家记录了一棵树1-5年的高度,由此建立的高度高与生长年数的回归模型为y=3.O01t-0.25用这个模型预测这棵树第8年时的高度,则正确的叙述是( )
| A、高度一定是23.83m |
| B、高度在23.83m左右 |
| C、高度在23.83m以下 |
| D、高度在23.83m以上 |
(
+
)50的二项展开式中,整数项的个数是( )
| 3 | 2 |
| 1 | ||
|
| A、3 | B、4 | C、5 | D、6 |
α=-
,则角α的终边在( )
| 2π |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某设备零件的三视图如图所示,则这个零件的体积为( )


| A、6 | B、8 | C、3 | D、4 |
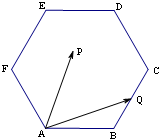 如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则
如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则