题目内容
18.已知函数f(x)=x+$\frac{a}{x}$+a2-2,a∈R(Ⅰ)若f(x)是奇函数,且在区间(0,+∞)上是增函数,求a的值
(Ⅱ)设g(x)=f(1)-a2+|log8(x+1)|,若g(x)在区间(-1,1)内有两个不同的零点m,n,求a的取值范围,并求$\frac{1}{m}$$+\frac{1}{n}$的值.
分析 (I)根据奇函数的性质可得a=$±\sqrt{2}$,令f′(x)≥0在(0,+∞)上恒成立可得出a的范围,从而得出a的值;
(II)令g(x)=0可得|log8(x+1)|=a-1,作出y=|log8(x+1)|的函数图象,根据图象即可得出a-1的范围,从而得出a的范围,根据g(m)=g(n)=0得出m,n的关系,利用对数的运算性质化简即可得出$\frac{1}{m}$$+\frac{1}{n}$的值.
解答 解:(I)∵f(x)是奇函数,∴f(x)+f(-x)=0,
即a2-2=0,解得a=±$\sqrt{2}$.
∵f(x)在(0,+∞)上是增函数,
∴f′(x)≥0在(0,+∞)上恒成立,即1-$\frac{a}{{x}^{2}}$≥0在(0,+∞)上恒成立,
∴a≤x2在(0,+∞)上恒成立,∴a≤0.
∴a=-$\sqrt{2}$.
(II)g(x)=f(1)-a2+|log8(x+1)|=a-1+|log8(x+1)|,
令g(x)=0得|log8(x+1)|=1-a,则方程|log8(x+1)|=1-a在(-1,1)上有两解,
作出y=|log8(x+1)|的函数图象如图所示:
∵方程|log8(x+1)|=1-a在(-1,1)上有两解,
∴0<1-a<$\frac{1}{3}$,即$\frac{2}{3}$<a<1.
设m<n,则-1<m<0<n<1,
∵g(m)=g(n)=0,
∴log8(m+1)+log8(n+1)=0,即(m+1)(n+1)=1,
∴mn+m+n=0,
∴$\frac{1}{m}+\frac{1}{n}=-1$.
点评 本题考查了函数单调性、奇偶性的性质,函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
3.函数f(x)=sin($\frac{π}{3}$-2x)的单调递增区间是( )
| A. | [-kπ-$\frac{π}{12}$,-kπ+$\frac{5π}{12}$],k∈Z | B. | [2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$],k∈Z | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z |
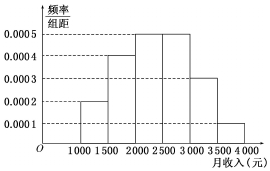 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).