题目内容
11.已知公差不为0的等差数列{an},若a2+a4=10,且a1、a2、a5成等比数列,则a1=1,an=2n-1.分析 设等差数列{an}的公差为d≠0,由a2+a4=10,且a1、a2、a5成等比数列,可得a22=a1a5,即(a1+d)2=a1(a1+4d),解得a1,d即可得出.
解答 解:设等差数列{an}的公差为d≠0,∵a2+a4=10,且a1、a2、a5成等比数列,
则2a1+4d=10,
a22=a1a5,即(a1+d)2=a1(a1+4d),
解得a1=1,d=2.
∴an=1+2(n-1)=2n-1.
故答案为:1,an=2n-1.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.抛物线y2=4x的焦点到双曲线x2-$\frac{{y}^{2}}{2}$=1的渐近线的距离等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
3. 如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
 如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | ($\frac{\sqrt{6}}{3}$,$\sqrt{2}$) |
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,O为坐标原点,M为长轴的一个端点,若在椭圆上存在点N,使ON⊥MN,则离心率e的取值范围为( )
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
 对于任意
对于任意 恒成立;
恒成立;  ,如果命题“
,如果命题“ 为真,
为真, 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.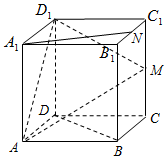 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,