题目内容
2．已知四棱锥P-ABCD的底面是正方形，PA⊥平面ABCD，且PA=AD，则平面PAB与平面PCD所成的二面角的度数为450．分析 如图，过点P作直线l∥AB，直线l就是平面PAB与平面PCD的交线，故∠DPA就是平面PAB与平面PCD所成的二面角的平面角，在直角△PAD△中可知∠DPA=45°．
解答 解：如图，过点P作直线l∥AB，直线l就是平面PAB与平面PCD的交线，
∵PA⊥面ABCD，∴PA⊥CD，又∵CD⊥AD，∴CD⊥面PAD
即CD⊥PD，∴PD⊥l，PA⊥l，故∠DPA就是平面PAB与平面PCD所成的二面角的平面角，
在直角△PAD△中可知∠DPA=45°．
故答案为：450
点评 本题考查了二面角的求解，属于基础题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
4．设i为虚数单位，若复数$\frac{i}{1+i}$的实部为a，复数（1+i）2的虚部为b，则复数z=a-bi在复平面内的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
的图象大致是（ ）
B．
C．
D．
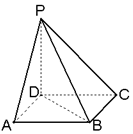如图，已知ABCD是正方形，PD⊥平面ABCD，PD=AD．
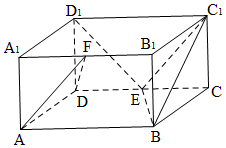已知四棱柱ABC-A1B1C1D1的底面是边长为2的菱形，且∠BAD=$\frac{π}{3}$，AA1⊥平面ABCD，设E为CD的中点
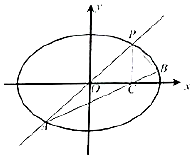如图所示，已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$过点$（{\sqrt{2}，\sqrt{2}}）$，直线l：y=kx（k≠0）与椭圆E交于P、A两点，过点P作PC⊥x轴，垂足为C点，直线AC交椭圆E与另一点B，当$k=\sqrt{2}$时，椭圆E的右焦点到直线l的距离为$\sqrt{2}$．