题目内容
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,O为坐标原点,M为长轴的一个端点,若在椭圆上存在点N,使ON⊥MN,则离心率e的取值范围为( )| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
分析 由ON⊥MN,可知$\overrightarrow{ON}$•$\overrightarrow{MN}$=x(x-a)+y2=0,代入椭圆方程,求得b和c的关系,利用离心率公式和离心率取值范围,即可求得e的取值范围.
解答 解:椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,焦点在x轴上,设M(a,0),N(x,y),则$\overrightarrow{ON}$=(x,y),$\overrightarrow{MN}$=(x-a,y).
由ON⊥MN,
∴$\overrightarrow{ON}$•$\overrightarrow{MN}$=x(x-a)+y2=0
由椭圆方程得y2=b2-$\frac{{b}^{2}}{{a}^{2}}$x2代入得c2x2-a3x+a2b2=0.
解得:x=a,或x=$\frac{a{b}^{2}}{{c}^{2}}$,
由题意0<$\frac{a{b}^{2}}{{c}^{2}}$<a.
∴b2<c2.
∴a2-c2<c2.
解得e2=$\frac{{c}^{2}}{{a}^{2}}$>$\frac{1}{2}$,
∵0<e<1
∴$\frac{\sqrt{2}}{2}$<e<1.
离心率e的取值范围为($\frac{\sqrt{2}}{2}$,1).
故选:A.
点评 本题考查椭圆的标准方程及简单几何性质,考查向量与圆锥关系的综合应用,考查计算能力,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
8.四面体ABCD中∠BAC=∠BAD=∠CAD=60°,AB=2,AC=3,AD=4,则四面体ABCD的体积V=( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
15. 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )| A. | 168 | B. | 169 | C. | 170 | D. | 171 |
9.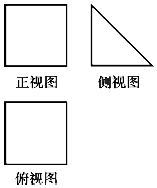 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
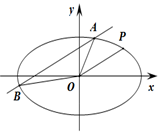 如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.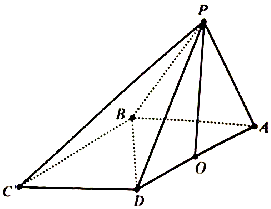 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.