题目内容
16.已知数列{an}的前n项和为Sn,数列{$\frac{{S}_{n}}{n}$}的公差为1的等差数列,且a2=3,a3=5.(1)求数列{an}的通项公式;
(2)设bn=an•3n,求数列{bn}的前n项和Tn.
分析 (1)数列{$\frac{{S}_{n}}{n}$}的公差为1的等差数列,可得$\frac{{S}_{n}}{n}$=a1+n-1,Sn=n(a1+n-1),分别取n=2,3,及其a2=3,a3=5.解得a1=1.可得Sn=n2.利用递推关系即可得出.
(2)bn=an•3n=(2n-1)•3n,利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)数列{$\frac{{S}_{n}}{n}$}的公差为1的等差数列,∴$\frac{{S}_{n}}{n}$=a1+n-1,可得Sn=n(a1+n-1),
∴a1+a2=2(a1+1),a1+a2+a3=3(a1+2),且a2=3,a3=5.
解得a1=1.
∴Sn=n2.
∴n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1(n=1时也成立).
∴an=2n-1.
(2)bn=an•3n=(2n-1)•3n,
∴数列{bn}的前n项和Tn=3+3×32+5×33+…+(2n-1)•3n,
∴3Tn=32+3×33+…+(2n-3)•3n+(2n-1)•3n+1,
∴-2Tn=3+2×(32+33+…+3n)-(2n-1)•3n+1=3+2×$\frac{9({3}^{n-1}-1)}{3-1}$-(2n-1)•3n+1,
可得Tn=3+(n-1)•3n+1.
点评 本题考查了数列递推关系、“错位相减法”与等比数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.四面体ABCD中∠BAC=∠BAD=∠CAD=60°,AB=2,AC=3,AD=4,则四面体ABCD的体积V=( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围为___________.
的取值范围为___________.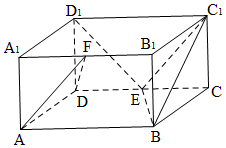 已知四棱柱ABC-A1B1C1D1的底面是边长为2的菱形,且∠BAD=$\frac{π}{3}$,AA1⊥平面ABCD,设E为CD的中点
已知四棱柱ABC-A1B1C1D1的底面是边长为2的菱形,且∠BAD=$\frac{π}{3}$,AA1⊥平面ABCD,设E为CD的中点 如图,在边长为4的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1E⊥EB.
如图,在边长为4的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1E⊥EB.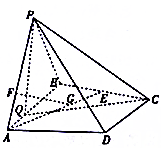 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,△PAB为正三角形,AB⊥AD,CD⊥AD,点E为线段BC的中点,F,G分别为线段PA,AE上一点,且AB=AD=2,PF=2FA.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,△PAB为正三角形,AB⊥AD,CD⊥AD,点E为线段BC的中点,F,G分别为线段PA,AE上一点,且AB=AD=2,PF=2FA.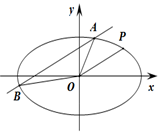 如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.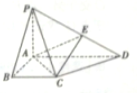 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.