题目内容
1.已知函数f(x)=axex-(a-1)(x+1)2(其中a∈R,e为自然对数的底数,e=2.718128…).(1)当a=-1时,求f(x)的单调区间;
(2)若f(x)仅有一个极值点,求a的取值范围.
分析 (1)根据导数和函数的单调性的关系即可求出,
(2)先求导,再令f'(x)=0得到x=-1或aex-2a+2=0(*),根据aex-2a+2=0(*)无解即可求出a的范围.
解答 解:(1)由题知,f(x)=-xex+2(x+1)2,
f'(x)=-ex-xex+4(x+1)=(x+1)(4-ex),
由f'(x)=0得到x=-1或x=ln4,
而当x<ln4时,(4-ex)>0,x>ln4时,(4-ex)<0,列表得:
| x | (-∞,-1) | -1 | (-1,ln4) | ln4 | (ln4,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极大值 | ↗ | 极小值 | ↘ |
(2)f'(x)=aex+axex-2(a-1)(x+1)=(x+1)(aex-2a+2),
由f'(x)=0得到x=-1或aex-2a+2=0(*)
由于f(x)仅有一个极值点,
关于x的方程(*)必无解,
①当a=0时,(*)无解,符合题意,
②当a≠0时,由(*)得${e^x}=\frac{2a-2}{a}$,故由$\frac{2a-2}{a}≤0$得0<a≤1,
由于这两种情况都有,当x<-1时,f'(x)<0,于是f(x)为减函数,
当x>-1时,f'(x)>0,于是f(x)为增函数,
∴仅x=-1为f(x)的极值点,
综上可得a的取值范围是[0,1].
点评 本题考查了导数和函数的单调性和关系和一级函数的极值的问题,考查了分类讨论的思想,属于中档题

练习册系列答案
相关题目
9.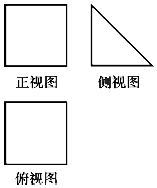 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
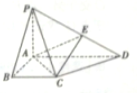 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.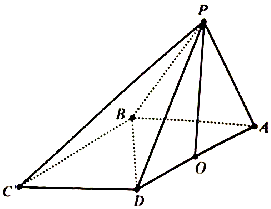 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O. 如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.