题目内容
3. 如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | ($\frac{\sqrt{6}}{3}$,$\sqrt{2}$) |
分析 以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出线段PA长的取值范围.
解答  解:以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,
解:以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,
建立空间直角坐标系,
则A(0,1,1),B(0,2,0),C(0,0,0),
设Q(q,0,0),$\overrightarrow{AP}=λ\overrightarrow{AB}$=(0,λ,-λ),
则$\overrightarrow{PQ}$=$\overrightarrow{CQ}$-$\overrightarrow{CP}$=$\overrightarrow{CQ}-(\overrightarrow{CA}+\overrightarrow{AP})$=(q,0,0)-(0,1,1)-(0,λ,-λ)=(q,-1-λ,λ-1),
∵异面直线PQ与AC成30°的角,
∴cos30°=$\frac{|\overrightarrow{CA}•\overrightarrow{PQ}|}{|\overrightarrow{CA}|•|\overrightarrow{PQ}|}$=$\frac{2}{\sqrt{2}•\sqrt{{q}^{2}+(1+λ)^{2}+(λ-1)^{2}}}$=$\frac{\sqrt{2}}{\sqrt{{q}^{2}+2{λ}^{2}+2}}$=$\frac{\sqrt{3}}{2}$,
∴q2+2λ2+2=$\frac{8}{3}$,∴${q}^{2}=\frac{2}{3}-2{λ}^{2}∈[0,4]$,
∴$\left\{\begin{array}{l}{\frac{2}{3}-2{λ}^{2}≥0}\\{\frac{2}{3}-2{λ}^{2}≤4}\end{array}\right.$,解得0$≤λ≤\frac{\sqrt{3}}{3}$,
∴|$\overrightarrow{AP}$|=$\sqrt{2}λ$∈[0,$\frac{\sqrt{6}}{3}$],
∴线段PA长的取值范围是[0,$\frac{\sqrt{6}}{3}$].
故选:B.
点评 本题考查线段的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
 的图象大致是( )
的图象大致是( ) B.
B. C.
C. D.
D.
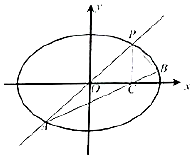 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$. 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )