题目内容
等差数列{an}、{bn}的前n项和为Sn，Tn，若
=
，则
= ．
| Sn |
| Tn |
| 2n+2 |
| n+3 |
| a9 |
| b4 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意和等差数列前n项和的特点，设出两数列的前n项和分别为Sn=kn（2n+2），Tn=kn（n+3）（k≠0），由关系式：n≥2时，an=Sn-Sn-1求出它们的通项公式，再求出
的值即可．
| a9 |
| b4 |
解答：
解：因为等差数列{an}{bn}的前n项和为Sn、Tn，且
=
，
所以设Tn=kn（n+3），Sn=kn（2n+2））（k≠0），则
当n≥2时，an=Sn-Sn-1=4kn，当n=1时也满足，则an=4kn；
当n≥2时，bn=Tn-Tn-1=2k（n+1），当n=1时也满足，则bn=2k（n+1），
所以
=
=
，
故答案为：
．
| Sn |
| Tn |
| 2n+2 |
| n+3 |
所以设Tn=kn（n+3），Sn=kn（2n+2））（k≠0），则
当n≥2时，an=Sn-Sn-1=4kn，当n=1时也满足，则an=4kn；
当n≥2时，bn=Tn-Tn-1=2k（n+1），当n=1时也满足，则bn=2k（n+1），
所以
| a9 |
| b4 |
| 4k×9 |
| 2k×5 |
| 18 |
| 5 |
故答案为：
| 18 |
| 5 |
点评：本题考查等差数列的通项公式、前n项和公式的应用，求出等差数列{an}，{bn}的通项，是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某几何体的三视图是如图所示，其中左视图为半圆，则该几何体的体积是（ ）
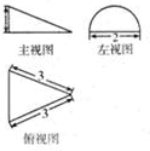
A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
某校男女篮球队各有10名队员，现将这20名队员的身高绘制成如图所示茎叶图（单位：cm）．男队员身高在180cm以上定义为“高个子”，女队员身高在170cm以上定义为“高个子”，其他队员定义为“非高个子”．用分层抽样的方法，从“高个子”和“非高个子”中共抽取5名队员．