题目内容
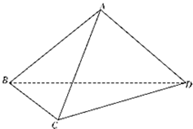 A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.(1)求证:AB⊥CD;
(2)求AB与平面BCD所成角的余弦值.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由已知可得△ABC≌△ABD,BC=BD.取CD的中点M,连接AM,BM,可得CD⊥AM,CD⊥BM,可得CD⊥平面ABM,即可证明.
(2)过点A作AO⊥BM于点O,由CD⊥平面ABM,可得平面BCD⊥平面ABM,于是AO⊥平面BCD,因此∠ABO是AB与平面BCD所成角.在△ABC中,利用余弦定理可得BC.在RT△BCM中,BM=
.再利用余弦定理可得cos∠ABM=
.
(2)过点A作AO⊥BM于点O,由CD⊥平面ABM,可得平面BCD⊥平面ABM,于是AO⊥平面BCD,因此∠ABO是AB与平面BCD所成角.在△ABC中,利用余弦定理可得BC.在RT△BCM中,BM=
| BC2-CM2 |
| AB2+BM2-AM2 |
| 2AB•BM |
解答:
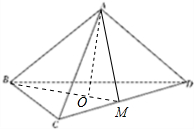 (1)证明:∵∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(1)证明:∵∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
∴△ABC≌△ABD,BC=BD.
取CD的中点M,连接AM,BM,则CD⊥AM,CD⊥BM,
又AM∩BM=M,∴CD⊥平面ABM,
∴AB⊥CD.
(2)解:过点A作AO⊥BM于点O,∵CD⊥平面ABM,
∴平面BCD⊥平面ABM,
∴AO⊥平面BCD,
∴∠ABO是AB与平面BCD所成角.
在△ABC中,BC2=AB2+AC2-2AB•AC•cos∠BAC=7,
∴BC=
.
∵△ACD是等边三角形,∴AM=
.
在RT△BCM中,BM=
=
.
在△ABM中,由余弦定理可得:cos∠ABM=
=
.
 (1)证明:∵∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(1)证明:∵∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.∴△ABC≌△ABD,BC=BD.
取CD的中点M,连接AM,BM,则CD⊥AM,CD⊥BM,
又AM∩BM=M,∴CD⊥平面ABM,
∴AB⊥CD.
(2)解:过点A作AO⊥BM于点O,∵CD⊥平面ABM,
∴平面BCD⊥平面ABM,
∴AO⊥平面BCD,
∴∠ABO是AB与平面BCD所成角.
在△ABC中,BC2=AB2+AC2-2AB•AC•cos∠BAC=7,
∴BC=
| 7 |
∵△ACD是等边三角形,∴AM=
| 3 |
在RT△BCM中,BM=
| BC2-CM2 |
| 6 |
在△ABM中,由余弦定理可得:cos∠ABM=
| AB2+BM2-AM2 |
| 2AB•BM |
| ||
| 3 |
点评:本题考查了空间线面面面位置关系的判定及其性质、空间角的求法、余弦定理、等边三角形的性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知ω=-
+
i(i是虚数单位),(ωx+
)2015的展开式中系数为实数的项有( )
| 1 |
| 2 |
| ||
| 2 |
. |
| ω |
| A、671项 | B、672项 |
| C、673项 | D、674项 |
已知f(x)=
,g(x)=2lnx,曲线y=f(x)在点(1,f(1))处的切线方程为2x-y-2=0.
(1)求a,b的值;
(2)若当x≥1时,g(x)≤mf(x)恒成立,求m的取值范围.
| ax2+b |
| x |
(1)求a,b的值;
(2)若当x≥1时,g(x)≤mf(x)恒成立,求m的取值范围.
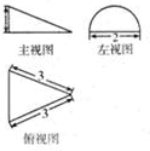
某几何体的三视图是如图所示,其中左视图为半圆,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
已知集合A={x|(x+1)(x-2)≥0},则∁RA=( )
| A、{x|x<-1,或x>2} |
| B、{x|x≤-1,或x≥2} |
| C、{x|-1<x<2} |
| D、{x|-1≤x≤2} |
