题目内容
(1)已知tanσ=
,求
的值;
(2)已知sinσ+3cosσ=0,求sinσ,cosσ的值.
| 1 |
| 2 |
| 1+2sin(π-σ)cos(-2π-σ) | ||
sin2(-σ)-sin2(
|
(2)已知sinσ+3cosσ=0,求sinσ,cosσ的值.
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式利用诱导公式化简,再利用同角三角函数间基本关系变形,把tanσ的值代入计算即可求出值;
(2)由已知等式,利用同角三角函数间的基本关系求出sinσ与cosσ的值即可.
(2)由已知等式,利用同角三角函数间的基本关系求出sinσ与cosσ的值即可.
解答:
解:(1)原式=
=
=
=
=
=-3;
(2)∵sinσ=-3cosσ,
又sin2σ+cos2σ=1,得(-3cosσ)2+cos2σ=1,即10cos2σ=1,
∴cosσ=±
,
又由sinσ=-3cosσ,可知sinσ与cosσ异号,
∴σ在第二、四象限.
①当σ是第二象限角时,sinσ=
,cosσ=-
;
②当σ是第四象限角时,sinσ=-
,cosσ=
.
| 1+2sinσcosσ |
| sin2σ-cos2σ |
| (sinσ+cosσ)2 |
| (sinσ+cosσ)(sinσ-cosσ) |
| sinσ+cosσ |
| sinσ-cosσ |
| 1+tanσ |
| tanσ-1 |
1+
| ||
|
(2)∵sinσ=-3cosσ,
又sin2σ+cos2σ=1,得(-3cosσ)2+cos2σ=1,即10cos2σ=1,
∴cosσ=±
| ||
| 10 |
又由sinσ=-3cosσ,可知sinσ与cosσ异号,
∴σ在第二、四象限.
①当σ是第二象限角时,sinσ=
3
| ||
| 10 |
| ||
| 10 |
②当σ是第四象限角时,sinσ=-
3
| ||
| 10 |
| ||
| 10 |
点评:此题考查了运用诱导公式化简求值,以及同角三角函数基本关系的运用,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设M,P是两个非空集合,定义M与P的差集为M-P={x|x∈M且x∉P},则M-(M-P)等于( )
| A、P | B、M∩P | C、M∪P | D、M |
下列函数中,既是奇函数又是减函数的是( )
| A、y=-x3 |
| B、y=cos x |
| C、y=sinx |
| D、y=-ex |
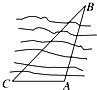 某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
α、β均为锐角,cosβ=
,cos(α+β)=
,则cosα的值为( )
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
设函数f(x)=
sin(2x+
),向左平移
个单位得到函数g(x)的图象,则( )
| 2 |
| π |
| 4 |
| π |
| 8 |
| A、g(x)是奇函数 |
| B、g(x)是偶函数 |
| C、g(x)是非奇非偶函数 |
| D、g(x)的奇偶性无法判断 |