题目内容
已知函数g(x)=
,x∈(0,+∞).
(1)若g(x)在(0,1)上是减函数,在[1,+∞)上的增函数,求实数b的值;
(2)若(1)的条件下,若g(x)的最小值是1,求函数g(x)的解析式.
| x2+ax+b |
| x |
(1)若g(x)在(0,1)上是减函数,在[1,+∞)上的增函数,求实数b的值;
(2)若(1)的条件下,若g(x)的最小值是1,求函数g(x)的解析式.
考点:导数在最大值、最小值问题中的应用,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)由已知得g(x)=x+a+
,g(x)在x=1时取得最小值,由此利用基本不等能求出实数b的值为1.
(2)由(1)知g(x)的最小值为a+2当g(x)的最小值为1时,a+2=1,由此能求出g(x)=
.
| b |
| x |
(2)由(1)知g(x)的最小值为a+2当g(x)的最小值为1时,a+2=1,由此能求出g(x)=
| x2-x+1 |
| x |
解答:
解:(1)∵g(x)=
,x∈(0,+∞),
∴g(x)=x+a+
,
∵g(x)在(0,1)上是减函数,在[1,+∞)上是增函数,
∴g(x)在x=1时取得最小值,
∵g(x)=(x+
)+a≥2
+a=2
+a,
∴当x=
=1时取得最小值,所以有b=1,
实数b的值为1.
(2)由(1)知g(x)的最小值为a+2
∴当g(x)的最小值为1时,
a+2=1,解得a=-1,
所以g(x)=
.
| x2+ax+b |
| x |
∴g(x)=x+a+
| b |
| x |
∵g(x)在(0,1)上是减函数,在[1,+∞)上是增函数,
∴g(x)在x=1时取得最小值,
∵g(x)=(x+
| b |
| x |
x•
|
| b |
∴当x=
| b |
| x |
实数b的值为1.
(2)由(1)知g(x)的最小值为a+2
∴当g(x)的最小值为1时,
a+2=1,解得a=-1,
所以g(x)=
| x2-x+1 |
| x |
点评:本题考查实数值的求法,考查函数的解析式的求法,是中档题,解题时要认真审题,注意函数性质和均值不等式的合理运用.

练习册系列答案
相关题目
设M,P是两个非空集合,定义M与P的差集为M-P={x|x∈M且x∉P},则M-(M-P)等于( )
| A、P | B、M∩P | C、M∪P | D、M |
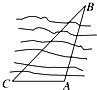 某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )