题目内容
若△ABC的三边为a，b，c，它的面积为
，那么内角C等于 ．
| a2+b2-c2 | ||
4
|
考点：余弦定理
专题：解三角形
分析：通过三角形的面积结合余弦定理，直接求解即可．
解答：
解：∵三角形的面积为：
absinC，
由题意∴
absinC=
，
可得cosC=
=
sinC，
∴tanC=
，C是三角形内角，
∴C=30°．
故答案为：30°．
| 1 |
| 2 |
由题意∴
| 1 |
| 2 |
| a2+b2-c2 | ||
4
|
可得cosC=
| a2+b2-c2 |
| 2ab |
| 3 |
∴tanC=
| ||
| 3 |
∴C=30°．
故答案为：30°．
点评：本题考查余弦定理以及同角三角函数的基本关系式的应用，考查计算能力．
练习册系列答案
相关题目
下列函数中，既是奇函数又是减函数的是（ ）
| A、y=-x3 |
| B、y=cos x |
| C、y=sinx |
| D、y=-ex |
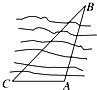某地决定修建一条长为AB的跨河大桥，如图，A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测得AC的距离为am，∠ACB=45°，∠CAB=105°，则A、B两点的距离为（ ）