题目内容
(1)已知α,β都为锐角,sinα=
,cos(α+β)=
,求sinβ与cosβ的值;
(2)已知0<β<
<α<π,且cos(α-
)=-
,sin(
-β)=
,求cos(α+β)的值.
| 1 |
| 7 |
5
| ||
| 14 |
(2)已知0<β<
| π |
| 2 |
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:(1)已知α,β都为锐角,sinα=
,先求出cosα的值,由cos(α+β)=
,用两角和的余弦公式化简后即可解得sinβ与cosβ的值;
(2)已知0<β<
<α<π,且cos(α-
)=-
,sin(
-β)=
,先求出sin(α-
)=
,cos(
-β)=
,即可求出sin(
+
)的值,再由cos(α+β)=1-2sin(
+
)sin(
+
)即可求出cos(α+β)的值.
| 1 |
| 7 |
5
| ||
| 14 |
(2)已知0<β<
| π |
| 2 |
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
| β |
| 2 |
4
| ||
| 9 |
| α |
| 2 |
| ||
| 3 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
解答:
解:(1)已知α,β都为锐角,sinα=
,有cosα=
=
,
cos(α+β)=
,故有cosαcosβ-sinαsinβ=
,即有8
cosβ-2sinβ=5
.
令cosβ=A,则sinβ=
,代入上式整理得,196A2-240A+71=0,
解得A=
=
,故A1=
,A2=
.
即:cosβ=
或
.
则:sinβ=
=
或
.
∵cosβ=
,sinβ=
代入8
cosβ-2sinβ=5
中不成立,故舍去.
∴cosβ=
,sinβ=
.
(2)∵0<β<
<α<π
∴
<α-
<π;-
<
-β<
∵cos(α-
)=-
,sin(
-β)=
,
∴sin(α-
)=
,cos(
-β)=
sin(
+
)=sin[(α-
)-(
-β)]=sin(α-
)cos(
-β)-cos(α-
)sin(
-β)=
cos(α+β)=1-2sin(
+
)sin(
+
)=-
.
| 1 |
| 7 |
| 1-sin2α |
4
| ||
| 7 |
cos(α+β)=
5
| ||
| 14 |
5
| ||
| 7 |
| 3 |
| 3 |
令cosβ=A,则sinβ=
| 1-A2 |
解得A=
240±
| ||
| 392 |
| 240±44 |
| 392 |
| 71 |
| 98 |
| 1 |
| 2 |
即:cosβ=
| 71 |
| 98 |
| 1 |
| 2 |
则:sinβ=
| 1-A2 |
39
| ||
| 98 |
| ||
| 2 |
∵cosβ=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
∴cosβ=
| 71 |
| 98 |
39
| ||
| 98 |
(2)∵0<β<
| π |
| 2 |
∴
| π |
| 4 |
| β |
| 2 |
| π |
| 4 |
| α |
| 2 |
| π |
| 2 |
∵cos(α-
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
∴sin(α-
| β |
| 2 |
4
| ||
| 9 |
| α |
| 2 |
| ||
| 3 |
sin(
| α |
| 2 |
| β |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| 22 |
| 27 |
cos(α+β)=1-2sin(
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| 239 |
| 729 |
点评:本题主要考察两角和与差的正弦函数、余弦函数和计算能力,属于中档题.

练习册系列答案
相关题目
下列函数中,为偶函数的是( )
A、f(x)=sin(
| ||
B、f(x)=cos(
| ||
C、f(x)=tan(
| ||
D、f(x)=sin(
|
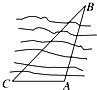 某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )