题目内容
16．m＜2是方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-1}$=1表示双曲线的必要不充分条件．（从“充分必要”，“充分不必要”，“必要不充分”，“既不充分也不必要”中选择一个正确的填写）．分析 由方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-1}$=1表示双曲线，则（m-2）（m-1）＜0，解得m范围即可判断出．
解答 解：若方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-1}$=1表示双曲线，则（m-2）（m-1）＜0，解得1＜m＜2．
∴m＜2是方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-1}$=1表示双曲线的必要不充分条件．
故答案为：必要不充分．
点评 本题考查了直线系的应用、斜率的意义，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
7．
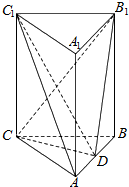如图所示，三棱柱ABC-A1B1C1中，CC1⊥平面ABC，△ABC是边长为2的等边三角形，D为AB边的中点，且CC1=2AB．
（Ⅰ）求证：AC1∥平面CDB1．
（Ⅱ）求点B到平面B1CD的距离．
如图所示，三棱柱ABC-A1B1C1中，CC1⊥平面ABC，△ABC是边长为2的等边三角形，D为AB边的中点，且CC1=2AB．（Ⅰ）求证：AC1∥平面CDB1．
（Ⅱ）求点B到平面B1CD的距离．
1．集合A={1，2}，B={1，2，3}，则下列关系正确的是（ ）
| A． | A=B | B． | A∩B=∅ | C． | A⊆B | D． | A?B |