题目内容

6．如图所示，最左边的几何体由一个圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得，现用一个竖直的平面去截这个几何体，则截面图形可能是（　　）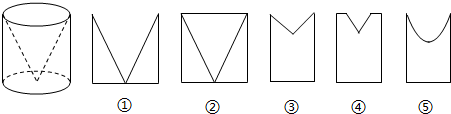
A．①②B．②③C．③④D．①⑤

分析 根据圆锥曲线的定义和圆锥的几何特征，分截面过旋转轴时和截面不过旋转轴时两种情况，分析截面图形的形状，最后综合讨论结果，可得答案

解答 解：当截面过旋转轴时，
圆锥的轴截面为等腰三角形，此时（1）符合条件；
当截面不过旋转轴时，
圆锥的轴截面为双曲线的一支，此时（5）符合条件；
故截面图形可能是（1）（5），
故选：D．

点评 本题考查的知识点是旋转体，圆锥曲线的定义，熟练掌握圆锥曲线的定义是解答的关键．

练习册系列答案
相关题目
16．已知双曲线方程$\frac{x^2}{4}-\frac{y^2}{5}$=1，则它的焦点到渐近线的距离为（　　）
A．$\sqrt{5}$B．1C．2D．$\sqrt{3}$
17．已知集合A={-1，0}，集合B={0，1，x+2}，且A∩B={0，-1}，则实数x的值为-3．
14．若函数f（x）=$\frac{x+a}{{e}^{x}}$在区间（-∞，2）上为单调递增函数，则实数a的取值范围是（　　）
A．[0，+∞）B．（0，e]C．（-∞，-1]D．（-∞，-e）
1．斜率为1的直线经过抛物线y2=4x的焦点，且与抛物线相交于A，B两点，则|AB|=（　　）
A．8B．6C．12D．7$\sqrt{3}$
11．点A（-2，3）关于直线l：3x-y-1=0的对称点坐标是（4，1）．
18．已知直线l，m，平面α，且l⊥α，则l⊥m是m?α的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
15．已知圆（x+1）2+y2=2，则其圆心和半径分别为（　　）
A．（1，0），2B．（-1，0），2C．$（1，0），\sqrt{2}$D．$（-1，0），\sqrt{2}$
16．m＜2是方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{m-1}$=1表示双曲线的必要不充分条件．（从“充分必要”，“充分不必要”，“必要不充分”，“既不充分也不必要”中选择一个正确的填写）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网