题目内容
7.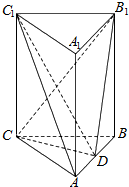 如图所示,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边的中点,且CC1=2AB.
如图所示,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边的中点,且CC1=2AB.(Ⅰ)求证:AC1∥平面CDB1.
(Ⅱ)求点B到平面B1CD的距离.
分析 (Ⅰ)连接BC1交B1C于点O,连接DO,由三角形中位线的性质得DO∥AC1,从而证明AC1∥平面CDB1,
(Ⅱ)等体积法,三棱锥D-CBB1的体积和三棱锥B1-CBD体积相等,BB1为三棱锥D-CBB1的高,△CBB1是直角三角形,面积可求,体积可求,再求得${S}_{△{B}_{1}CD}$,即可得解点B到平面B1CD的距离.
解答  证明:(Ⅰ)证明:连接BC1交B1C于点O,连接DO.
证明:(Ⅰ)证明:连接BC1交B1C于点O,连接DO.
则O是BC1的中点,DO是△BAC1的中位线.
所以DO∥AC1.
因为DO?平面CDB1,AC1?平面CDB1,
所以AC1∥平面CDB1.
(Ⅱ)解:因为CC1⊥平面ABC,
所以BB1⊥平面ABC.
所以BB1为三棱锥D-CBB1的高.
VD-CBB1=VB1-CBD=$\frac{1}{3}$S△BCD•BB1=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{4}×{2}^{2}×4=\frac{2\sqrt{3}}{3}$.
所以三棱锥D-CBB1的体积为$\frac{2\sqrt{3}}{3}$.
因为:B1D=$\sqrt{{B}_{1}{B}^{2}+B{D}^{2}}$=$\sqrt{17}$,CD=$\sqrt{C{A}^{2}-A{D}^{2}}$=$\sqrt{3}$,B1C=$\sqrt{B{C}^{2}+B{{B}_{1}}^{2}}$=2$\sqrt{5}$,
由余弦定理可求cos∠B1CD=$\frac{20+3-17}{2×2\sqrt{5}×\sqrt{3}}$=$\frac{\sqrt{15}}{10}$,sin∠B1CD=$\frac{\sqrt{85}}{10}$,
则可得:${S}_{△{B}_{1}CD}$=$\frac{1}{2}$×B1C×CD×sin∠B1CD=$\frac{\sqrt{51}}{2}$,
所以,点B到平面B1CD的距离d=3×$\frac{\frac{2\sqrt{3}}{3}}{\frac{\sqrt{51}}{2}}$=$\frac{4\sqrt{17}}{17}$.
点评 本题考查面面垂直的判定、线面平行的判定,用等体积法求三棱锥的体积,考查了空间想象能力和推理论证能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (1,0),2 | B. | (-1,0),2 | C. | $(1,0),\sqrt{2}$ | D. | $(-1,0),\sqrt{2}$ |
| A. | ?x>0,x3≤0 | B. | $?{x_0}≤0,x_0^3≤0$ | C. | ?x<0,x3≤0 | D. | $?{x_0}>0,x_0^3≤0$ |
 如图,四边形ABCD是矩形,AB=1,AD=$\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD
如图,四边形ABCD是矩形,AB=1,AD=$\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD