题目内容
5.已知函数f(x)=sinx,$g(x)=\left\{\begin{array}{l}-\;\frac{1}{x},\;\;x<0\\ lgx,\;\;\;x>0\end{array}\right.$,则函数h(x)=f(x)-g(x)在区间[-2π,4π]内的零点个数为5.分析 由h(x)=f(x)-g(x)=0.得f(x)=g(x),作出函数f(x)和g(x)的图象,利用数形结合进行判断即可.
解答  解:由h(x)=f(x)-g(x)=0.得f(x)=g(x),
解:由h(x)=f(x)-g(x)=0.得f(x)=g(x),
作出函数f(x)和g(x)的图象如图:
由图象知两个函数在区间[-2π,4π]内的交点个数为5个,
即函数h(x)=f(x)-g(x)在区间[-2π,4π]内的零点个数为5个,
故答案为:5.
点评 本题主要考查函数与方程的应用,根据条件转化为两个函数的交点问题是解决本题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
15.已知圆(x+1)2+y2=2,则其圆心和半径分别为( )
| A. | (1,0),2 | B. | (-1,0),2 | C. | $(1,0),\sqrt{2}$ | D. | $(-1,0),\sqrt{2}$ |
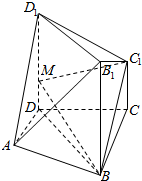 如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.
如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.