题目内容
4.袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为$\frac{2}{3}$.分析 先求出基本事件总数,再求出这2只球颜色不同,包含的基本事件个数,由此能求出这2只球颜色不同的概率.
解答 解:袋中有形状、大小都相同的4只球,其中2只红球,2只黄球,从中一次随机摸出2只球,
基本事件总数n=${C}_{4}^{2}$=6,
这2只球颜色不同,包含的基本事件个数m=C${\;}_{2}^{1}$${C}_{2}^{1}$=4,
∴这2只球颜色不同的概率p=$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.若函数f(x)=$\frac{x+a}{{e}^{x}}$在区间(-∞,2)上为单调递增函数,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (0,e] | C. | (-∞,-1] | D. | (-∞,-e) |
15.已知圆(x+1)2+y2=2,则其圆心和半径分别为( )
| A. | (1,0),2 | B. | (-1,0),2 | C. | $(1,0),\sqrt{2}$ | D. | $(-1,0),\sqrt{2}$ |
19.已知命题p:?x>0,x3>0,那么¬p是( )
| A. | ?x>0,x3≤0 | B. | $?{x_0}≤0,x_0^3≤0$ | C. | ?x<0,x3≤0 | D. | $?{x_0}>0,x_0^3≤0$ |
 如图,四边形ABCD是矩形,AB=1,AD=$\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD
如图,四边形ABCD是矩形,AB=1,AD=$\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD
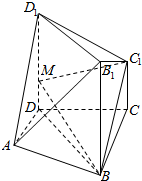 如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.
如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.