题目内容
6.(1+2x)n(其中n∈N+且n≥6)的展开式中x3与x4项的二项式系数相等,则系数最大项为672x5.分析 (1+2x)n(其中n∈N+且n≥6)的展开式中,Tr+1=${∁}_{n}^{r}$(2x)r=2r${∁}_{n}^{r}$xr,又x3与x4项的二项式系数相等,可得${∁}_{n}^{3}$=${∁}_{n}^{4}$,解得n=7.由$\left\{\begin{array}{l}{{2}^{r+2}{∁}_{7}^{r+2}≤{2}^{r+1}{∁}_{7}^{r+1}}\\{{2}^{r+1}{∁}_{7}^{r+1}≥{2}^{r}{∁}_{7}^{r}}\end{array}\right.$,解得:r即可得出.
解答 解:(1+2x)n(其中n∈N+且n≥6)的展开式中,Tr+1=${∁}_{n}^{r}$(2x)r=2r${∁}_{n}^{r}$xr,
又x3与x4项的二项式系数相等,
∴${∁}_{n}^{3}$=${∁}_{n}^{4}$,
解得n=7.
∴Tr+1=2r${∁}_{7}^{r}$xr.
由$\left\{\begin{array}{l}{{2}^{r+2}{∁}_{7}^{r+2}≤{2}^{r+1}{∁}_{7}^{r+1}}\\{{2}^{r+1}{∁}_{7}^{r+1}≥{2}^{r}{∁}_{7}^{r}}\end{array}\right.$,解得:r=4.
则系数最大项为第5项.
T5=${2}^{5}{∁}_{7}^{5}$x5=672x5.
故答案为:672x5.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设函数f(x)=3|x-1|-2x+a,g(x)=2-x2,若在区间(0,3)上,f(x)的图象在g(x)的图象的上方,则实数a的取值范围为( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (3,+∞) | D. | [3,+∞) |
16.已知圆C的方程为x2+y2-4x=0,则圆心C到直线y=$\frac{x}{2}$+1的距离为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
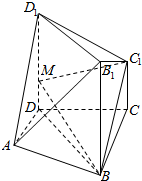 如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.
如图:几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.