题目内容
已知tanα=3，求
的值．
| 4sinα-3cosα |
| 7sinα+3cosα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式分子分母除以cosα，利用同角三角函数间基本关系弦化切后，把tanα的值代入计算即可求出值．
解答：
解：∵tanα=3，
∴原式=
=
=
．
∴原式=
| 4tanα-3 |
| 7tanα+3 |
| 12-3 |
| 21+3 |
| 3 |
| 8 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
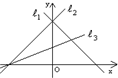
如图所示，直线l1，l2，l3的斜率分别为k1，k2，k3，则（ ）
| A、k1＜k2＜k3 |
| B、k3＜k1＜k2 |
| C、k1＜k3＜k2 |
| D、k3＜k2＜k1 |
已知全集U=R，A={x|2x＜1}，B={x|y=lg（2-x）}，则（∁UA）∩B=（ ）
| A、（1，2] |
| B、（1，2） |
| C、（0，2] |
| D、[0，2） |
已知函数f（x）=x2+2bx的图象在点O（0，0）处的切线l与直线x-y+3=0平行，若数列{
}的前n项和为Sn，则S2014=（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a，b为正实数，且a+b=1，则log2a+log2b的最大值为（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|