题目内容
7.某厂每月生产一种投影仪的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年需求量为500台,销售的收入函数为R(x)=5x-$\frac{x^2}{2}$(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台).(1)求月销售利润y(万元)关于月产量x(百台)的函数解析式;
(2)当月产量为多少时,销售利润可达到最大?最大利润为多少?
分析 (1)分类讨论:①当0≤x≤5时,②当x>5时,分别写出函数f(x)的表达式,最后利用分段函数的形式写出所求函数解析式即可;
(2)分别求出当0≤x≤5时,及当x>5时,f(x)的最大值,最后综上所述,当x为多少时,f(x)有最大值.
解答 解:(1)当0≤x≤5时,投影仪能售出x百台;
当x>5时,只能售出5百台,这时成本为(0.5+0.25x)万元.…(2分)
依题意可得利润函数为y=R(x)-(0.5+0.25x)=$\left\{{\begin{array}{l}{(5x-\frac{x^2}{2})-(0.5+0.25x),(0≤x≤5)}\\{(5×5-\frac{5^2}{2})-(0.5+0.25x),(x>5)}\end{array}}\right.$…(5分)
即 $y=\left\{{\begin{array}{l}{4.75x-\frac{x^2}{2}-0.5,(0≤x≤5)}\\{12-0.25x,(x>5)}\end{array}}\right.$.…(7分)
(2)显然,y|x>5<y|x=5;…(8分)
又当0≤x≤5时,$y=-\frac{1}{2}{(x-4.75)^2}+\frac{1}{2}×{4.75^2}-0.5$…(10分)
∴当x=4.75(百台)时有${y_{max}}=\frac{1}{2}×{4.75^2}-0.5=10.78125$(万元)
即当月产量为475台时可获得最大利润10.78125万元.…(12分)
点评 本题考查了分段函数,以及函数与方程的思想,属于基础题.函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.

| A. | 椭圆 | |
| B. | 椭圆和双曲线的一支 | |
| C. | 双曲线和一条直线(去掉几个点) | |
| D. | 双曲线的一支和一条直线(去掉几个点) |
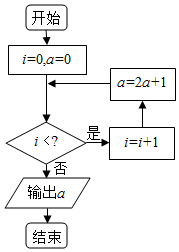
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | $\frac{5}{3}或\frac{4}{3}$ | B. | $\frac{{4\sqrt{7}}}{7}或\frac{4}{3}$ | C. | $\frac{{4\sqrt{7}}}{7}$ | D. | $\frac{4}{3}$ |
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
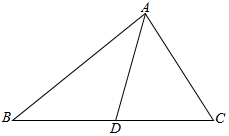 如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.
如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.