题目内容
已知函数f（x）=
，若存在两个不相等的实数x1，x2，使得f（x1）=f（x2），则实数a的取值范围为 ．
|
考点：分段函数的应用
专题：函数的性质及应用
分析：若函数f（x）=
，若存在两个不相等的实数x1，x2，使得f（x1）=f（x2），则函数不为单调函数，进而根据二次函数和一次函数的图象和性质，可得实数a的取值范围．
|
解答：
解：若存在两个不相等的实数x1，x2，使得f（x1）=f（x2），
则函数f（x）函数不为单调函数，
由y=-x2+2ax在（a，+∞）上为减函数，
故函数f（x）=
为单调函数时只能是减函数，
此时a＜0，
故函数f（x）函数不为单调函数时，a≥0，
即实数a的取值范围为：[0，+∞），
故答案为：[0，+∞）
则函数f（x）函数不为单调函数，
由y=-x2+2ax在（a，+∞）上为减函数，
故函数f（x）=
|
此时a＜0，
故函数f（x）函数不为单调函数时，a≥0，
即实数a的取值范围为：[0，+∞），
故答案为：[0，+∞）
点评：本题考查的知识点是分段函数的应用，其中根据已知分析出函数f（x）函数不为单调函数，是解答的关键．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
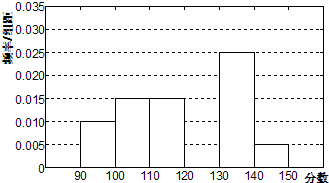武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图．观察图形的信息，回答如下问题：如果椭圆的两个顶点为（3，0），（0，4），则其标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
要得到函数y=sin(2x-
)的图象，可以将函数y=sin2x图象经何种变换得到（ ）
| π |
| 3 |
A、右移
| ||
B、右移
| ||
C、左移
| ||
D、左移
|