题目内容

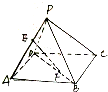如图，P是?ABCD所在平面外一点，E、F分别在PA、BD上，且PE：EA=BF：FD，求证：EF∥平面PBC．
考点：直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：在AB上取一点G，使AG：GB=AE：EP，则GF∥AD，则GF∥BC，可得FG∥平面PBC，再证明EG∥平面PBC，利用面面平行的判定可得平面EGF∥平面PBC，从而可得EF∥平面PBC．
解答： 证明：如图所示，在AB上取一点G，使AG：GB=AE：EP，则GF∥AD，
∵AD∥BC，∴GF∥BC，
∵GF?平面PBC，BC?平面PBC，
∴FG∥平面PBC，
∵BF：FD=BG：GA，GF∥AD，
∴AE：EP=AG：GB，
∴EG∥PB，
∵EG?平面PBC，PB?平面PBC，
∴EG∥平面PBC，
∵EG∩GF=G，
∴平面EGF∥平面PBC，
∵EF?平面EGF，
∴EF∥平面PBC．
点评：本题考查线面平行、面面平行的判定，考查学生分析解决问题的能力，属于基本知识的考查，属于中档题．
练习册系列答案
相关题目
2与10的等差中项是
 
．
数列{an}前n项和为Sn，已知a1=
2
3
，且对任意正整数m，n，都有am+n=am•an，若Sn＜a恒成立则实数a的最小值为（　　）
A、
1
2
B、
2
3
C、
3
2
D、2
直线y=a与曲线y=sin（x+
π
3
）在（0，2π）内有两个不同交点，求实数a取值范围．
已知方程x3-
2
9
x2+6x-a=0有且只有一个实数根，求实数a的取值范围．
设△ABC的内角A、B、C所对边的长分别为a、b、c，且B=
π
3
．
（1）若△ABC的面积为
3
3
4
，b=
3
，求a，c的值；
（2）若△ABC不是钝角三角形，求
2a
c
的取值范围．
已知α，β是两个不同的平面，l，m，n是不同的直线，则正确命题为（　　）
A、若l⊥m，l⊥n，m?α，n?α，则l⊥α
B、若l∥m，m?α，则l∥α
C、若α⊥β，α∩β=l，m?α，m⊥l，则m⊥β
D、若α⊥β，l⊥α，则l∥β
已知椭圆M的左右焦点分别为F1（-
3
，0），F2（
3
，0），且抛物线x2=4y的焦点为椭圆M的顶点，过点P（0，2）的直线l与椭圆交于不同的两点A、B．
（1）求椭圆M的方程；
（2）求△OAB面积的取值范围；
（3）若S△OAB=
4
5
，是否存在大于1的常数m，使得椭圆M上存在点Q，满足
OQ
=m（
OA
+
OB
）？若存在，试求出m的值；若不存在，说明理由．
若从5名男歌手和4名女歌手中各选一人参加“星光大道”节目，则不同的选法种数是（　　）
A、5种B、4种C、9种D、20种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网