题目内容

设△ABC的内角A、B、C所对边的长分别为a、b、c，且B=
π
3
．
（1）若△ABC的面积为
3
3
4
，b=
3
，求a，c的值；
（2）若△ABC不是钝角三角形，求
2a
c
的取值范围．
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）△ABC中，由题意可得可得
1
2
ac•sinB=
3
3
4
，且b2=3=a2+c2-2ac•cosB，化简可得ac=3，且a2+c2-ac=3，由此求得a、c的值．
（2）若△ABC不是钝角三角形，则C∈（
π
6
，
π
2
），利用正弦定理可得
2a
c
=
2sin(
2π
3
-C)
sinC
=
3
•
1
tanC
+1，由此求得
2a
c
的取值范围．
解答： 解：（1）△ABC中，由△ABC的面积为
3
3
4
，b=
3
，B=
π
3
，
可得
1
2
ac•sinB=
3
3
4
，且b2=3=a2+c2-2ac•cosB，
化简可得ac=3，且a2+c2-ac=3，求得a=c=
3
．
（2）若△ABC不是钝角三角形，则C∈（
π
6
，
π
2
），
∴tanC∈（
3
3
，+∞），
1
tanC
∈（0，
3
）．
∵B=
π
3
，故由正弦定理可得
2a
c
=
2sinA
sinC
=
2sin(
2π
3
-C)
sinC
=
3
cosC+sinC
sinC

=
3
•
1
tanC
+1∈（1，4），
即
2a
c
的取值范围为（1，4）．
点评：本题主要考查正弦定理、余弦定理的应用，正切函数的定义域和值域，属于基础题．
练习册系列答案
相关题目
若{1，2}⊆A⊆{1，2，3，4，5 }，则集合A的个数是
 
．
（1）（2
4
5
）0+2-2×（2
1
4
）- 
1
2
-（0.01） 
1
2
；
（2）2（lg
2
）2+lg
2
•lg5+
(lg
2
)2-lg2+1
．
下面四个命题：
①分别在两个平面内的直线平行
②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面
③如果一个平面内的两条直线平行于另一个平面，则这两个平面平行
④如果一个平面内的任何一条直线平行于另一个平面，则这两个平面平行
其中正确的命题是（　　）
A、①②B、②④C、①③D、②③
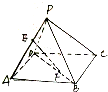如图，P是?ABCD所在平面外一点，E、F分别在PA、BD上，且PE：EA=BF：FD，求证：EF∥平面PBC．
设函数f（x）=
ex-1
x
．
（1）求函数f（x）在[
1
2
，2]上的最值；
（2）证明：对任意正数a，存在正数x，使不等式f（x）-1＜a成立．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点P（1，
3
2
），F1、F2分别为其左、焦点，直线l为其右准线．
（1）若2≤a≤
22
2
，求离心率e的取值范围；
（2）椭圆C的离心率e=
1
2
，点M是直线l上一动点．
①若直线F1M交椭圆于S点，且F1S=SM，求∠F1SF2的余弦值；
②直线L上是否存在一点N，使得F1M⊥F2N，且MN=2
14
？若存在，请求出N点的坐标，若不存在，请说明理由．
已知定点A、B，且|AB|=6，动点P满足|PA|-|PB|=4，则PA的最小值为
 
．
若向量
a
，
b
满足：|
a
|=1，（
a
+
b
）⊥
a
，（2
a
+
b
）⊥
b
，则|
b
|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网