题目内容
设f(x)=
,则f′(2)=( )
| x2+1 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:导数的运算
专题:导数的概念及应用
分析:根据复合函数的求导法则,先求导,再求值.
解答:
解:f′(x)=
(x2+1)-
•(2x),
∴f′(2)=
•5-
•2×2=
.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
∴f′(2)=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 5 |
故选:C.
点评:本题考查了复合函数的求导法则,属于基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
f(x)=
则f[f(
)]=( )
|
| 1 |
| 4 |
| A、9 | ||
B、
| ||
| C、1 | ||
| D、3 |
若
=k,则
等于( )
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0+2•△x)-f(x0) |
| △x |
| A、2k | ||
| B、k | ||
C、
| ||
| D、以上都不是 |
将函数y=2sinxsin(
+x)的图象向右平移φ(φ>0)个单位长度,使平移后的图象仍过点(
,
),则φ的最小值为( )
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若a>b,c∈R,则下列关系一定成立的是( )
| A、ac2>bc2 | ||||
| B、ac>bc | ||||
| C、a+c>b+c | ||||
D、
|
在空间直角坐标系中,已知点P(5,-1,4),则点P关于Z轴的对称点为( )
| A、P′(5,-1,-4) |
| B、P′(-5,-1,-4) |
| C、P′(-5,1,4) |
| D、P′(-5,1,-4) |
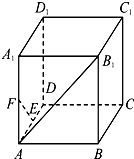
 如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为
如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为