题目内容
在平面内与点A（1，2）距离为1，与点B（4，1）距离为2的直线共有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
考点：点到直线的距离公式,两点间距离公式的应用
专题：直线与圆
分析：由题意把问题转化为两圆的公切线条数，只需判断圆的位置关系即可．
解答：
解：∵在平面内与点A（1，2）距离为1的直线
是以（1，2）为圆心1为半径的圆的切线，
同理可得与点B（4，1）距离为2的直线
是以（4，1）为圆心2为半径的圆的切线，
∴满足条件的直线为两圆的公切线，
∵|AB|=
=
＞1+2，
∴两圆的位置关系为外离，公切线有4条，
故满足条件的直线有4条，
故选：D
是以（1，2）为圆心1为半径的圆的切线，
同理可得与点B（4，1）距离为2的直线
是以（4，1）为圆心2为半径的圆的切线，
∴满足条件的直线为两圆的公切线，
∵|AB|=
| (1-4)2+(2-1)2 |
| 10 |
∴两圆的位置关系为外离，公切线有4条，
故满足条件的直线有4条，
故选：D
点评：本题考查点到直线的距离，转化为两圆的公切线是解决问题的关键，属中档题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知2a+b=1，a＞0，b＞0，则
+
的最小值是（ ）
| 1 |
| a |
| 1 |
| b |
A、2
| ||
B、3-2
| ||
C、3+2
| ||
D、3+
|
若双曲线与椭圆
+
=1有共同的焦点，且与椭圆相交，其中一个交点A的纵坐标为4，则双曲线的方程为（ ）
| x2 |
| 27 |
| y2 |
| 36 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}，{bn}，它们的前n项和分别为An，Bn，记cn=anBn+bnAn-anbn（n∈N*），则数列{cn}的前10项和为（ ）
| A、A10+B10 | ||
B、
| ||
| C、A10•B10 | ||
D、
|
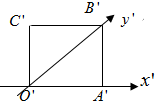如图所示，正方形O′A′B′C′的边长2cm，它是水平放置的一个平面图形的直观图，则原图形的周长是（ ）| A、16cm | ||
| B、8cm | ||
C、（2+3
| ||
D、（2+2
|
sin2013°的值属于区间（ ）
A、（
| ||
B、（0，
| ||
C、（-1，-
| ||
D、（-
|
不等式（
-x）（x-
）＞0的解集为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、{x|
| ||||
B、{x|x＞
| ||||
C、{x|x＜
| ||||
D、{x|x＜
|