题目内容
5．已知平面内一点p∈{（x，y）|（x-2cosθ）2+（y-2sinθ） 2=16，θ∈R}，则满足条件的点P在平面内所组成的图形的面积是（ ）| A． | 8π | B． | 16π | C． | 24π | D． | 32π |
分析 先根据圆的标准方程求出圆心和半径，然后研究圆心的轨迹，根据点P在平面内所组成的图形是一个环面求解得答案．
解答 解：由题意可知，P为圆（x-2cosα）2+（y-2sinα）2=16上的点，
而动圆（x-2cosα）2+（y-2sinα）2=16的圆心坐标为（2cosα，2sinα）半径为4，
圆心为以（0，0）为圆心，半径为2的圆上动点，
∴满足条件的点P在平面内的轨迹为圆环面，如图：
所组成的图形的面积是以原点为圆心，以6为半径的圆的面积减去以原点为圆心，以2为半径的圆的面积．
即36π-4π=32π．
故选：D．
点评 本题主要考查轨迹方程的求法，考查了圆的参数方程，正确理解题意是解题的关键，属于中档题．
练习册系列答案
相关题目
我国的《洛书》中记载着世界上最古老的幻方：将1，2，…，9填入方格内，使三行、三列，两条对角线的三个数之和都等于15，如图所示．
15．
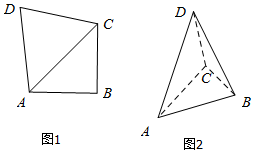如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC=$\sqrt{6}$．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）
如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC=$\sqrt{6}$．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）| A． | $\frac{9}{2}π$ | B． | $\frac{{8\sqrt{2}}}{3}π$ | C． | $\frac{27}{2}π$ | D． | 12π |