题目内容

方程x2+（k-2）x+5-k=0的两个不等实根都大于2，则实数k的取值范围是（　　）
A、k＜-2
B、k≤-4
C、-5＜k≤-4
D、-5＜k＜-4
考点：根与系数的关系
专题：函数的性质及应用
分析：设f（x）=x2+（k-2）x+5-k，由题意利用二次函数的性质求出k的范围．
解答： 解：令f（x）=x2+（k-2）x+5-k，由题意可得
△=(k-2)2-4(-k)＞0
x1+x2
2
=
2-k
2
＞2
f(2)=4+(k-2)×2+5-k＞0
，
解得-5＜k＜-4，
故选：D．
点评：本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
已知a＞0，函数f（x）=x3+ax2+bx+c在区间[-2，2]单调递减，则4a+b的最大值为
 
．
已知集合M={x|
2
x
＞1}，N={y|y=x2+1}，则M∩N=（　　）
A、[1，2）B、（1，2）
C、（2，+∞）D、∅
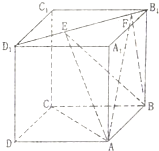如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=
2
2
，现有下列结论：
①AC⊥BE；
②平面AEF与平面ABCD的交线平行于直线EF；
③异面直线AE，BF所成的角为定值；
④三棱锥A-BEF的体积为定值，其中错误结论的个数是（　　）
A、0个B、1个C、2个D、3个
直线ax-y+3=0与圆（x-1）2+（y-2）2=4相交于A、B两点，且弦AB的长为2
3
，则a=（　　）
A、-1
B、0
C、
1
2
D、1
已知数列{an}对任意m，n∈N+都有am+n=am+an+3，若a1=3，则数列{an}的通项公式an=（　　）
A、6n-3B、4n-1
C、2n+1D、3n
从学号为1～60的高一某班60名学生中随机选取5名同学参加数学测试，采用系统抽样的方法，则所选5名学生的学号可能是（　　）
A、10，20，30，40，50
B、6，18，30，42，54
C、2，4，6，8，10
D、4，13，22，31，40
从装有n+1个球的口袋中取出m个球（0＜m≤n，m，n∈N），共有C
 
m
n+1
种取法．在这C
 
m
n+1
种取法中，可以分成一个指定的球被取到和未被取到两类：一类是该指定的球未被取到，共有C
 
0
1
•C
 
m
n
种取法；另一类是该指定的球被取到，共有C
 
1
1
•C
 
m-1
n
种取法．显然C10•Cnm+C11•Cnm-1=C
 
m
n+1
，即有等式：C
 
m
n
+C
 
m-1
n
=C
 
m
n+1
成立．试根据上述思想，则有：Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k（其中当1≤k＜m≤n，k，m，n∈N）为（　　）
A、C
 
m
n+k
B、C
 
m
n+k+1
C、C
 
m+1
n+k
D、C
 
k
n+m
下面多面体中有12条棱的是（　　）
A、四棱柱B、四棱锥
C、五棱锥D、五棱柱

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网