题目内容
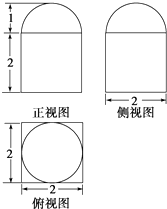 某个几何体的三视图如图所示(单位:m),
某个几何体的三视图如图所示(单位:m),(Ⅰ)说出该几何体的结构特征;
(Ⅱ)求该几何体的体积(结果保留π);
(Ⅲ)求该几何体的表面积(结果保留π).
考点:由三视图求面积、体积,简单空间图形的三视图,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(I)通过三视图判断几何体是一个组合体,上部为一个半径为1的半球,下部为棱长为2的正方体,
(II)该几何体的体积为正方体的体积+半球的体积;
(III)该几何体的表面积=正方体的表面积+半球面面积-球的底面积.
(II)该几何体的体积为正方体的体积+半球的体积;
(III)该几何体的表面积=正方体的表面积+半球面面积-球的底面积.
解答:
解:(I)由三视图可知,该几何体是由半球和正四棱柱组成,
棱柱是正方体棱长为2,球的半径为1,
(II)该几何体的体积为正方体的体积+半球的体积,
V=2×2×2+
×
×π×13=8+
π(m3)
(III)该几何体的表面积=正方体的表面积+半球面面积-球的底面积.
∴S=6×2×2+2π×12-π×12=24+π(m2).
棱柱是正方体棱长为2,球的半径为1,
(II)该几何体的体积为正方体的体积+半球的体积,
V=2×2×2+
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
(III)该几何体的表面积=正方体的表面积+半球面面积-球的底面积.
∴S=6×2×2+2π×12-π×12=24+π(m2).
点评:本题考查三视图复原几何体形状的判断,几何体的表面积与体积的求法,考查空间想象能力与计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数x,y满足
,则z=2x-y的取值范围是( )
|
| A、[1,7] |
| B、[-5,4] |
| C、[-5,7] |
| D、[4,7] |
假设某人在任何时间到达某十字路口是等可能的,已知路口的红绿灯,红灯时间为40秒,黄灯时间为3秒,绿灯时间为57秒,则此人到达路口恰好是红灯的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)=sin(2x+
)+cos(2x+
),则函数f(x)( )
| π |
| 4 |
| π |
| 4 |
A、图象关于直线x=
| ||
B、图象关于直线x=
| ||
C、图象关于直线x=
| ||
D、图象关于直线x=
|