题目内容
假设某人在任何时间到达某十字路口是等可能的，已知路口的红绿灯，红灯时间为40秒，黄灯时间为3秒，绿灯时间为57秒，则此人到达路口恰好是红灯的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：计算题,概率与统计
分析：本题是一个那可能事件的概率，试验发生包含的事件是总的时间长度为40+3+57=100秒，满足条件的事件是红灯的时间为40秒，根据等可能事件的概率得到答案．
解答：
解：由题意知本题是一个那可能事件的概率，
试验发生包含的事件是总的时间长度为40+3+57=100秒，
设红灯为事件A，满足条件的事件是红灯的时间为40秒，
根据等可能事件的概率得到
出现红灯的概率P（A）=
=
=
．
故选B．
试验发生包含的事件是总的时间长度为40+3+57=100秒，
设红灯为事件A，满足条件的事件是红灯的时间为40秒，
根据等可能事件的概率得到
出现红灯的概率P（A）=
| 构成事件A的时间长度 |
| 总的时间长度 |
| 40 |
| 100 |
| 2 |
| 5 |
故选B．
点评：本题考查等可能事件的概率，是一个由时间长度之比确定概率的问题，这是几何概型中的一种题目，是最基础的题．
练习册系列答案
相关题目
在△ABC中，a，b，c分别是内角A，B，C所对的边长，
=2
，
•
=0，
•
=-6，|
|=
．则内角B的大小为（ ）
| BD |
| DC |
| AB |
| AD |
| AB |
| BC |
| AD |
2
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若△ABC与△BDC同时内接于圆，则圆心O是这两个三角形的（ ）
| A、重心 | B、垂心 |
| C、外心 | D、重心和垂心 |
函数y=sin（x+
）的一个单调增区间是（ ）
| π |
| 4 |
| A、[-π，0] | ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
已知集合M={x|（x-1）2＞1，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A、{-1，3} |
| B、{-1，0，3} |
| C、{0，2，3} |
| D、{1，2，3} |
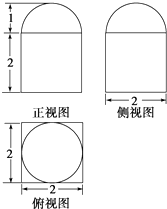某个几何体的三视图如图所示（单位：m），