题目内容
甲乙等五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务，每个岗位至少有一名志愿者．
（1）求一共有多少种不同的分配方案？
（2）对甲乙两人不在同一岗位的分配方法有多少种？
（1）求一共有多少种不同的分配方案？
（2）对甲乙两人不在同一岗位的分配方法有多少种？
考点：计数原理的应用
专题：排列组合
分析：（1）五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务，每个岗位至少有一名志愿者，则有且只有2人分在一组，先从5人中选2人分为一组，然后再平均分配到四个不同的岗位服务，问题得以解决．
（2）先求出甲乙两人在同一岗位的分配方法有，利用间接法，问题得以解决．
（2）先求出甲乙两人在同一岗位的分配方法有，利用间接法，问题得以解决．
解答：
解：（1）由题意得，有且只有2人分在一组，然后平均分到4个不同的岗位，则有
•
=240种不同的分配方案．
（2）利用间接法，甲乙两人在同一岗位的分配方法有
=24，由（1）知一共有240种不同的分配方案，
故甲乙两人不在同一岗位的分配方法有240-24=216种．
| C | 2 5 |
| A | 4 4 |
（2）利用间接法，甲乙两人在同一岗位的分配方法有
| A | 4 4 |
故甲乙两人不在同一岗位的分配方法有240-24=216种．
点评：本题主要考查了排列组合中的分配问题，关键是如何分组，属于中档题．
练习册系列答案
相关题目
在△ABC中，a，b，c分别是内角A，B，C所对的边长，
=2
，
•
=0，
•
=-6，|
|=
．则内角B的大小为（ ）
| BD |
| DC |
| AB |
| AD |
| AB |
| BC |
| AD |
2
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M={x|（x-1）2＞1，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A、{-1，3} |
| B、{-1，0，3} |
| C、{0，2，3} |
| D、{1，2，3} |
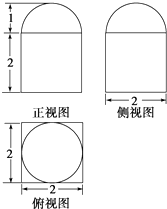某个几何体的三视图如图所示（单位：m），