题目内容
已知中心在原点，一焦点为F（0，
）的椭圆被直线l：y=3x-2截得的弦的中点横坐标为
．
（1）求此椭圆的方程；
（2）过定点M（0，9）的直线与椭圆有交点，求直线的斜率k的取值范围．
| 50 |
| 1 |
| 2 |
（1）求此椭圆的方程；
（2）过定点M（0，9）的直线与椭圆有交点，求直线的斜率k的取值范围．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）设椭圆为
+
=1，由已知条件推导出a2=b2+50，
=
，由此能求出椭圆．
（2）设过定点M（0，9）的直线为l，若斜率k不存在，直线l方程为x=0，与椭圆交点是椭圆的上顶点（0，5
）和下顶点（0，-5
）；若斜率k存在，直线l的方程为：y=kx+9，k≠0，代入椭圆方程，由△≥0，能求出直线的斜率k的取值范围．
| x2 |
| b2 |
| y2 |
| a2 |
| 6b2 |
| a2+9b2 |
| 1 |
| 2 |
（2）设过定点M（0，9）的直线为l，若斜率k不存在，直线l方程为x=0，与椭圆交点是椭圆的上顶点（0，5
| 3 |
| 3 |
解答：
解：（1）∵椭圆中心在原点，一焦点为F（0，
），
∴设椭圆为
+
=1，（a＞b＞0），
a2=b2+c2=b2+50，①
把y=3x-2代入椭圆方程，得
a2x2+b2（3x-2）2=a2b2，
（a2+9b2）x2-12b2x+4b2-a2b2=0，
∵椭圆被直线l：y=3x-2截得的弦的中点横坐标为
，
∴
=
，整理，得a2=3b2，②
由①②解得：a2=75，b2=25，
∴椭圆为：
+
=1．
（2）设过定点M（0，9）的直线为l，
①若斜率k不存在，直线l方程为x=0，与椭圆交点是椭圆的上顶点（0，5
）和下顶点（0，-5
）；
②若斜率k=0，直线l方程为y=9，与椭圆无交点；
③若斜率k存在且不为0时，直线l的方程为：y=kx+9，k≠0
联立
，得（3+k2）x2+18kx+6=0，
△=（18k）2-24（3+k2）≥0，
解得k≥
或k≤-
．
综上所述：直线的斜率k的取值范围k≥
或k≤-
或k不存在．
| 50 |
∴设椭圆为
| x2 |
| b2 |
| y2 |
| a2 |
a2=b2+c2=b2+50，①
把y=3x-2代入椭圆方程，得
a2x2+b2（3x-2）2=a2b2，
（a2+9b2）x2-12b2x+4b2-a2b2=0，
∵椭圆被直线l：y=3x-2截得的弦的中点横坐标为
| 1 |
| 2 |
∴
| 6b2 |
| a2+9b2 |
| 1 |
| 2 |
由①②解得：a2=75，b2=25，
∴椭圆为：
| x2 |
| 25 |
| y2 |
| 75 |
（2）设过定点M（0，9）的直线为l，
①若斜率k不存在，直线l方程为x=0，与椭圆交点是椭圆的上顶点（0，5
| 3 |
| 3 |
②若斜率k=0，直线l方程为y=9，与椭圆无交点；
③若斜率k存在且不为0时，直线l的方程为：y=kx+9，k≠0
联立
|
△=（18k）2-24（3+k2）≥0，
解得k≥
| ||
| 5 |
| ||
| 5 |
综上所述：直线的斜率k的取值范围k≥
| ||
| 5 |
| ||
| 5 |
点评：本题考查椭圆方程的求法，考查直线的斜率的取值范围的求法，解题时要认真审题，注意中点坐标公式的合理运用．
练习册系列答案
小学期末标准试卷系列答案
相关题目
已知x，y∈R，i为虚数单位，且x+yi=
，则x+y=（ ）
| 3+4i |
| 1+2i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若△ABC与△BDC同时内接于圆，则圆心O是这两个三角形的（ ）
| A、重心 | B、垂心 |
| C、外心 | D、重心和垂心 |
已知集合M={x|（x-1）2＞1，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A、{-1，3} |
| B、{-1，0，3} |
| C、{0，2，3} |
| D、{1，2，3} |
已知直线l的参数方程为
（t为参数），则直线l的普通方程为（ ）
|
| A、x-y-2=0 |
| B、x-y+2=0 |
| C、x+y=0 |
| D、x+y-2=0 |
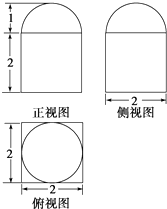某个几何体的三视图如图所示（单位：m），