题目内容
设f(x)=ax2+bx+c(a≠0),若函数f(x+1)与f(x)的图象关于y轴对称,求证:f(x+
)为偶函数.
| 1 |
| 2 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数的对称性,以及函数奇偶性的定义进行证明.
解答:
解:∵函数f(x+1)与f(x)的图象关于y轴对称,
∴f(x+1)=f(-x),
即f(x-
+1)=f[-(x-
)]
则f(x+
)=f(-x+
)
则f(x+
)为偶函数.
∴f(x+1)=f(-x),
即f(x-
| 1 |
| 2 |
| 1 |
| 2 |
则f(x+
| 1 |
| 2 |
| 1 |
| 2 |
则f(x+
| 1 |
| 2 |
点评:本题主要考查函数奇偶性的证明,根据函数的对称性得到f(x+1)=f(-x)是解决本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
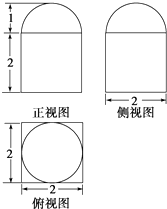 某个几何体的三视图如图所示(单位:m),
某个几何体的三视图如图所示(单位:m),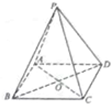 如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.
如图,三棱锥P-ABCD的底面ABCD是正方形,顶点P在底面的射影是AC与BD的交点O,AB=2,∠PAC=60°.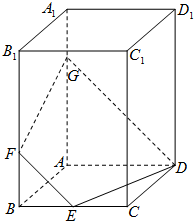 如图,ABCD-A1B1C1D1是长方体,AB=BC=2,E、F分别是棱BC、BB1上一点,BE=BF=1,经过D、E、F三点的平面与棱AA1相交于G.
如图,ABCD-A1B1C1D1是长方体,AB=BC=2,E、F分别是棱BC、BB1上一点,BE=BF=1,经过D、E、F三点的平面与棱AA1相交于G.