题目内容
设f（x）=sin（2x+
）+cos（2x+
），则函数f（x）（ ）
| π |
| 4 |
| π |
| 4 |
A、图象关于直线x=
| ||
B、图象关于直线x=
| ||
C、图象关于直线x=
| ||
D、图象关于直线x=
|
考点：三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：先利用两角和公式对函数解析式化简，进而令2x=kπ，求得函数的对称轴方程，对四个选项验证即可．
解答：
解：f（x）=
sin（2x+
+
）=
sin（2x+
）=
cos2x，
令2x=kπ，k∈Z，x=
，
∴函数的对称轴方程为x=
，
故只有C项中说法正确．
故选：C．
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
令2x=kπ，k∈Z，x=
| kπ |
| 2 |
∴函数的对称轴方程为x=
| kπ |
| 2 |
故只有C项中说法正确．
故选：C．
点评：本题主要考查了三角函数图象与性质．正弦函数和余弦函数图象的对称轴的位置都在函数取得最大或最小值的位置上．
练习册系列答案
金钥匙试卷系列答案
相关题目
函数y=sin（x+
）的一个单调增区间是（ ）
| π |
| 4 |
| A、[-π，0] | ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
已知集合M={x|（x-1）2＞1，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A、{-1，3} |
| B、{-1，0，3} |
| C、{0，2，3} |
| D、{1，2，3} |
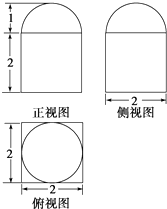某个几何体的三视图如图所示（单位：m），
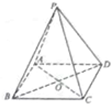如图，三棱锥P-ABCD的底面ABCD是正方形，顶点P在底面的射影是AC与BD的交点O，AB=2，∠PAC=60°．