题目内容
5.已知全集U={1,2,3,4,5,6,7},集合A={2,4,5},B={1,3,5,7},则(∁UA)∩B=( )| A. | {7} | B. | {3,5} | C. | {1,3,6,7} | D. | {1,3,7} |
分析 由补集定义先求出CUA,再由交集定义能求出(∁UA)∩B.
解答 解:∵全集U={1,2,3,4,5,6,7},
集合A={2,4,5},B={1,3,5,7},
∴CUA={1,3,6,7},
(∁UA)∩B={1,3,7}.
故选:D.
点评 本题考查的知识点是集合的交集,补集运算,集合的包含关系判断及应用,难度不大,属于基础题.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(cosx,-3),$\overrightarrow{b}$=(2cosx,$\frac{1}{3}$),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
16.等差数列{an}中,a2=8,前6项和和S6=66,设${b_n}=\frac{2}{{(n+1){a_n}}}$,Tn=b1+b2+…+bn,则Tn=( )
| A. | $1-\frac{1}{n+1}$ | B. | $1-\frac{1}{n+2}$ | C. | $\frac{1}{2}-\frac{1}{n+1}$ | D. | $\frac{1}{2}-\frac{1}{n+2}$ |
14.某大学有甲、乙两个图书馆,对其借书、还书的等待时间进行调查,得到下表:
甲图书馆
乙图书馆
以表中等待时间的学生人数的频率为概率.
(1)分别求在甲、乙两图书馆借书的平均等待时间;
(2)学校规定借书、还书必须在同一图书馆,某学生需要借一本数学参考书,并希望借、还书的等待时间之和不超过4分钟,在哪个图书馆借、还书更能满足他的要求?
甲图书馆
| 借(还)书等待时间T1(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1500 | 1000 | 500 | 500 | 1500 |
| 借(还)书等待时间T2(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1000 | 500 | 2000 | 1250 | 250 |
(1)分别求在甲、乙两图书馆借书的平均等待时间;
(2)学校规定借书、还书必须在同一图书馆,某学生需要借一本数学参考书,并希望借、还书的等待时间之和不超过4分钟,在哪个图书馆借、还书更能满足他的要求?
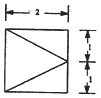 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数为( )
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数为( )