题目内容
15.已知向量$\overrightarrow{a}$=(cosx,-3),$\overrightarrow{b}$=(2cosx,$\frac{1}{3}$),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$,x∈R,则f(x)是( )| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
分析 根据向量数量积公式和三角恒等变换公式,化简得f(x)=cos2x,再利用三角函数的周期的公式,奇偶性的定义,即可得解.
解答 解:f(x)=$\overrightarrow{a}•\overrightarrow{b}=cosx•2cosx-3×\frac{1}{3}=2co{s}^{2}x-1$=cos2x,
∴f(x)的最小正周期为$\frac{2π}{2}$=π,满足f(-x)=f(x),故f(x)是偶函数.
故选:A
点评 本题考查了向量数量积运算、三角函数恒等变形、三角函数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知角α的终边与单位圆交于点(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$),则sin2α的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
10.求函数f(x)=x+$\frac{1}{x}$-1-ln(x+3)零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.执行如图所示的程序框图,则输出S的值为( )
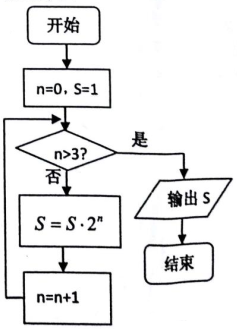

| A. | 16 | B. | 32 | C. | 64 | D. | 1024 |
5.已知全集U={1,2,3,4,5,6,7},集合A={2,4,5},B={1,3,5,7},则(∁UA)∩B=( )
| A. | {7} | B. | {3,5} | C. | {1,3,6,7} | D. | {1,3,7} |
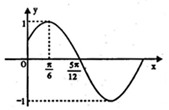 已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.
已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示. 图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.
图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.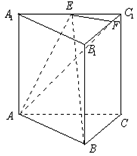 已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.
已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.