题目内容
13.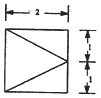 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数为( )
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由俯视图判断出PO⊥平面ABCD,由线面垂直的定义、判定定理判断出侧面中直角三角形的个数.
解答 解:由俯视图可得,PO⊥平面ABCD,
∴PO⊥AB,
∵AB⊥BC,且PO∩BC=O,
∴AB⊥PB,
同理可证,CD⊥PC,则△PAB、△PDC是直角三角形,
∵侧视图为直角三角形,
∴△PBC是直角三角形,且PC⊥PB,
∴四棱锥的侧面中直角三角形的个数是3,如图所示.
故选:C.
点评 本题考查了几何体三视图,线面垂直的定义、判定定理的应用问题,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.已知角α的终边与单位圆交于点(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$),则sin2α的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
1.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=xsinx+3 | B. | y=x3 | C. | y=-sinx | D. | y=-3x |
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线与抛物线x2=4y的准线所围成的三角形面积为2,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
5.已知全集U={1,2,3,4,5,6,7},集合A={2,4,5},B={1,3,5,7},则(∁UA)∩B=( )
| A. | {7} | B. | {3,5} | C. | {1,3,6,7} | D. | {1,3,7} |
2.已知A、B为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,点P在E上,在△APB中,tanA=$\frac{1}{3}$,tanB=$\frac{3}{4}$,则E的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
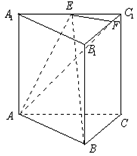 已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.
已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.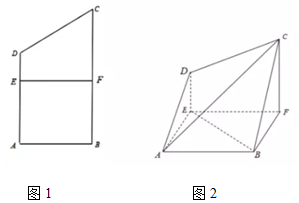 已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.
已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.