题目内容
下列说法中：①经过圆柱任意两条母线的截面是一个矩形；②连结圆柱上、下底面圆周上两点的线段是圆柱的母线；③圆柱的任意两条母线互相平行；④圆柱的侧面展开图是矩形；⑤圆柱的母线有且只有一条．其中正确命题的个数为（ ）
| A、3 | B、1 | C、2 | D、0 |
考点：命题的真假判断与应用
专题：阅读型,空间位置关系与距离
分析：矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．由定义及概念，可判断②⑤；再由性质，截面的形状，侧面展开图，即可判断①③④．
解答：
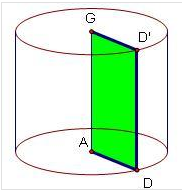解：如图矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．
故①经过圆柱任意两条母线的截面是一个矩形，则①对；
由母线定义可知②错；由圆柱的性质可知③对；
将圆柱沿着一条母线展开得到矩形，故④对；
⑤圆柱的母线有无数条，故⑤错．
故正确的命题的个数为3，
故选：A．
解：如图矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．故①经过圆柱任意两条母线的截面是一个矩形，则①对；
由母线定义可知②错；由圆柱的性质可知③对；
将圆柱沿着一条母线展开得到矩形，故④对；
⑤圆柱的母线有无数条，故⑤错．
故正确的命题的个数为3，
故选：A．
点评：本题考查圆柱的定义，性质和侧面展开图，以及截面等概念，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
已知函数f（x）=
，则满足f（x）=
的x的值为（ ）
|
| 1 |
| 2 |
A、
| ||||
| B、-1 | ||||
C、
| ||||
D、
|
已知F1，F2分别是椭圆C1和双曲线C2的公共的左右焦点，e1、e2是C1、C2的离心率，若C1、C2在第一象限内的交点为P，且满足∠POF2=2∠PF1F2，则e1、e2的关系是（ ）
| A、e12+e22=2e12e22 |
| B、e12+e1e2+e22=2 |
| C、e12+e22=2 |
| D、e1e2=2 |
如图，F1、F2是双曲线
某学校随机抽查了本校20个同学，调查他们平均每天在课外从事体育锻炼的时间（分钟），根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5），[5，10），…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是（ ）
已知“x＞2”是“x2＞a（a∈R）”的充分不必要条件，则a的取值范围是（ ）
| A、（-∞，4） |
| B、（4，+∞） |
| C、（0，4] |
| D、（-∞，4] |
定义在R上的函数f（x）=
，则f（x）（ ）
| x+1 | ||
|
| A、既有最大值也有最小值 |
| B、没有最大值，但有最小值 |
| C、有最大值，但没有最小值 |
| D、既没有最大值，也没有最小值 |
若α，β∈R，且α≠kπ+
（k∈Z），β≠kπ+
（k∈Z），则“α+β=
”是“（
tanα-1）（
tanβ-1）=4”的（ ）
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| 3 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |